
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)设F(x)=f(x)-f($\frac{2}{a}$-x),根据函数的单调性求出不等式的解集即可;
(Ⅲ)求出a>0,不妨设0<x1<$\frac{1}{a}$<x2,则$\frac{2}{a}$-x1∈($\frac{1}{a}$,+∞),根据函数的单调性得到f(x1)<f($\frac{2}{a}$-x1),由f(x1)=f(x2),替换即可.
解答 解:(I)f(x)的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
(1)当a≤0时,恒有f′(x)>0,故f(x)在(0,+∞)上单调递增;
(2)当a>0时,由f′(x)>0,得0<x<$\frac{1}{a}$,
故f(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,+∞)上单调递减,
综上(1)(2)可知:当a≤0时,f(x)的单调递增区间为(0,+∞);
当a>0时,f(x)的单调递增区间为(0,$\frac{1}{a}$),单调递减区间为($\frac{1}{a}$,+∞);
(II)f(x)的定义域为(0,+∞),所以x>0,且$\frac{2}{a}$-x>0,而a>0,0<x<$\frac{2}{a}$;
设F(x)=f(x)-f($\frac{2}{a}$-x)=lnx-ax-ln($\frac{2}{a}$-x)+a($\frac{2}{a}$-x)=lnx=ln($\frac{2}{a}$-x)-2ax+2,
F′(x)=$\frac{2{a(x-\frac{1}{a})}^{2}}{x(\frac{2}{a}-x)}$≥0,且当且仅当x=$\frac{1}{a}$时取等号,
所以F(x)在(0,$\frac{2}{a}$)上单调递增,又因为x=$\frac{1}{a}$时,F(x)=F($\frac{1}{a}$)=0,
所以当x∈(0,$\frac{1}{a}$)时,F(x)<0,当x∈($\frac{1}{a}$,$\frac{2}{a}$)时,F(x)>0,
故f(x)-f($\frac{2}{a}$-x)>0的解集为($\frac{1}{a}$,$\frac{2}{a}$);
(III)由(I)知a≤0时,f(x)在(0,+∞)上单调递增,若f(x1)=f(x2),
则x1=x2不合题意;
故a>0,而f(x)在(0,$\frac{1}{a}$)上单调递增,在($\frac{1}{a}$,+∞)上单调递减,
若存在两个不相等的正数x1,x2满足f(x1)=f(x2),
则x1,x2必有一个在(0,$\frac{1}{a}$)上,另一个在($\frac{1}{a}$,+∞),
不妨设0<x1<$\frac{1}{a}$<x2,则$\frac{2}{a}$-x1∈($\frac{1}{a}$,+∞),
又由(II)知x∈(0,$\frac{1}{a}$)时,F(x)<0,即f(x)-f($\frac{2}{a}$-x)<0,
所以f(x1)<f($\frac{2}{a}$-x1),
因为f(x1)=f(x2),所以f(x2)<f($\frac{2}{a}$-x1),
又因为f(x)在($\frac{1}{a}$,+∞)上单调递减,所以x2>$\frac{2}{a}$-x1,
即 x1+x2>$\frac{2}{a}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.
如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计).一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为$\frac{\sqrt{15}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
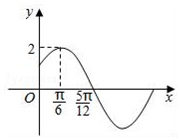 已知函数f(x)=Asin(ωx+φ)
已知函数f(x)=Asin(ωx+φ)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com