
设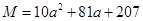 ,
,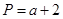 ,Q=
,Q=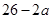 ;若将
;若将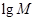 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列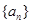 的前三项.
的前三项.
(1)试比较M、P、Q的大小;
(2)求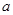 的值及
的值及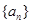 的通项;
的通项;
(3)记函数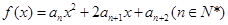 的图象在
的图象在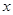 轴上截得的线段长为
轴上截得的线段长为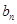 ,
,
设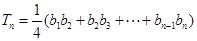
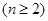 ,求
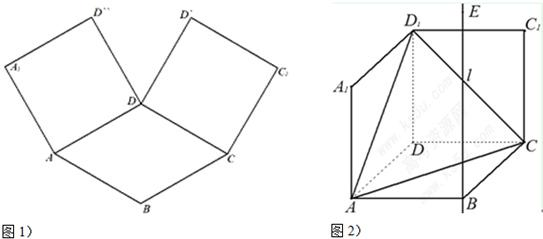
,求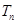 ,并证明
,并证明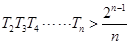 .
.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 3 |
| D1E |
查看答案和解析>>
科目:高中数学 来源: 题型:
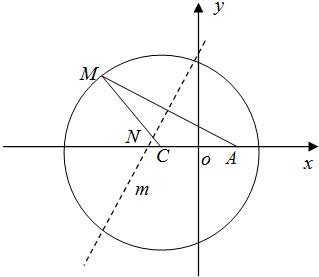 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.| 1 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三第二次教学质量考试数学理卷 题型:解答题
(本题满分14分)
如图1,在平面内,ABCD是 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).


(Ⅰ) 设二面角E – AC – D1的大小为q,若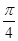 £ q £
£ q £  ,求线段BE长的取值范围;
,求线段BE长的取值范围;
(Ⅱ)在线段 上存在点
上存在点 ,使平面
,使平面 平面
平面 ,求
,求 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有 <
1.
<
1.
查看答案和解析>>
科目:高中数学 来源:2010-2010-2011学年四川省高三四月月考文科数学卷 题型:解答题
如图1,在平面内,ABCD是 且
且 的菱形,
的菱形, 和
和 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使 与
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。


(1)设二面角E – AC – D1的大小为q ,若 ,求
,求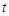 的取值范围;
的取值范围;
(2)在线段 上是否存在点
上是否存在点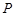 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出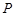 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图1,在平面内,ABCD是![]() 的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
的菱形,ADD``A1和CD D`C1都是正方形.将两个正方形分别沿AD,CD折起,使D``与D`重合于点D1 .设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧(图2).
(Ⅰ) 设二面角E – AC – D1的大小为q,若![]() £ q £
£ q £ ![]() ,求线段BE长的取值范围;
,求线段BE长的取值范围;

(第20题–1)

(第20题–2)
(Ⅱ)在线段![]() 上存在点
上存在点![]() ,使平面
,使平面![]() 平面
平面![]() ,求
,求![]() 与BE之间满足的关系式,并证明:当0 < BE < a时,恒有
与BE之间满足的关系式,并证明:当0 < BE < a时,恒有![]() < 1.
< 1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com