
 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为 ,最大数为
,最大数为 ;B组最小数为
;B组最小数为 ,最大数为
,最大数为 ,记
,记
 时,求
时,求 的分布列和数学期望;
的分布列和数学期望; 与
与 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率 ;
; 表示C的对立事件,判断
表示C的对立事件,判断 和
和 的大小关系,并说明理由。
的大小关系,并说明理由。 | 2 | 3 | 4 | 5 |
| P | 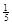 | 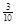 | 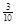 | 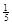 |
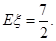 (2)当
(2)当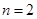 时,
时,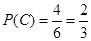 ,当
,当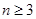 时
时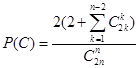
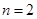 时,
时,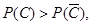 当
当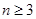 时,
时,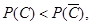
 时,将6个正整数平均分成A,B两组,不同的分组方法共有
时,将6个正整数平均分成A,B两组,不同的分组方法共有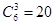 种,
种, 所有可能值为2,3,4,5.对应组数分别为4,6,6,4,对应概率为
所有可能值为2,3,4,5.对应组数分别为4,6,6,4,对应概率为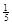 ,
,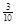 ,
,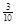 ,
,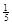 ,
,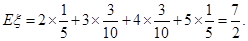 (2)
(2) 和
和 恰好相等的所有可能值为
恰好相等的所有可能值为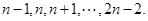 当
当 和
和 恰好相等且等于
恰好相等且等于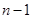 时,不同的分组方法有2种;当
时,不同的分组方法有2种;当 和
和 恰好相等且等于
恰好相等且等于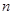 时,不同的分组方法有2种;当
时,不同的分组方法有2种;当 和
和 恰好相等且等于
恰好相等且等于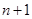 时,不同的分组方法有2
时,不同的分组方法有2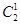 种;当
种;当 和
和 恰好相等且等于
恰好相等且等于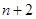 时,不同的分组方法有2
时,不同的分组方法有2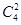 种;以此类推:
种;以此类推: 和
和 恰好相等且等于
恰好相等且等于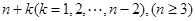 时,不同的分组方法有2
时,不同的分组方法有2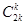 种;所以当
种;所以当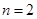 时,
时,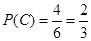
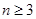 时
时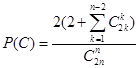 (3)先归纳:当
(3)先归纳:当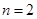 时,
时,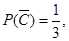 因此
因此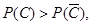 当
当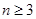 时,
时,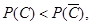 即证当
即证当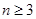 时
时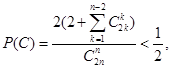
 ,这可用数学归纳法证明. 当
,这可用数学归纳法证明. 当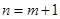 时,
时,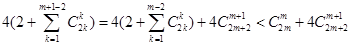 ,利用阶乘作差
,利用阶乘作差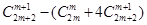 可得大小.
可得大小. 时,
时, 所有可能值为2,3,4,5.将6个正整数平均分成A,B两组,不同的分组方法共有
所有可能值为2,3,4,5.将6个正整数平均分成A,B两组,不同的分组方法共有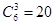 种,所以
种,所以 的分布列为
的分布列为 | 2 | 3 | 4 | 5 |
| P | 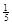 | 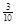 | 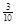 | 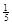 |
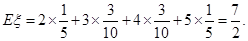
 和
和 恰好相等的所有可能值为
恰好相等的所有可能值为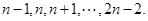
 和
和 恰好相等且等于
恰好相等且等于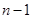 时,不同的分组方法有2种;
时,不同的分组方法有2种; 和
和 恰好相等且等于
恰好相等且等于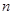 时,不同的分组方法有2种;
时,不同的分组方法有2种; 和
和 恰好相等且等于
恰好相等且等于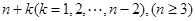 时,不同的分组方法有2
时,不同的分组方法有2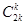 种;
种;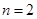 时,
时,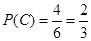
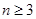 时
时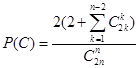
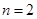 时,
时,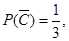 因此
因此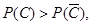
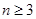 时,
时,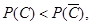 理由如下:
理由如下: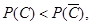 等价于
等价于 ①
①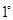 当
当 时,①式左边
时,①式左边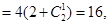 ①式右边
①式右边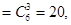 所以①式成立
所以①式成立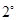 假设
假设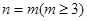 时①式成立,即
时①式成立,即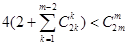 成立
成立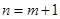 时,①式左边
时,①式左边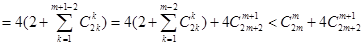
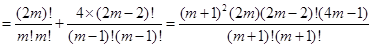
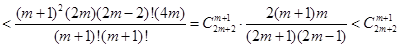 =①式右边
=①式右边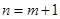 时①式也成立
时①式也成立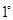
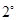 得,对于
得,对于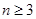 的所有正整数,都有
的所有正整数,都有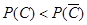 成立
成立

科目:高中数学 来源:不详 题型:单选题
| A.4 | B.3 | C.2 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 、
、 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 奖级 | 摸出红、蓝球个数 | 获奖金额 |
| 一等奖 | 3红1蓝 | 200元 |
| 二等奖 | 3红0蓝 | 50元 |
| 三等奖 | 2红1蓝 | 10元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com