[-3,5] 2

4
分析:(A)根据关于x的方程x
2+4x+|a-1|=0有实根,可得△≥0,解不等式即可求得结果;
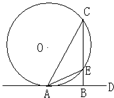
(B)根据AD为⊙O的切线,得出∠BAE=∠C,又AE平分∠CAB,得出∠BAC=2∠BAE,从而有∠BAE=∠C=30°最后利用特殊的直角三角形即可求出AC的长;
(C)把曲线C的极坐标方程化为普通方程,可知曲线是圆,根据点到直线的距离公式和圆被直线所截得的弦长公式进行计算.
解答:A:∵关于x的方程x
2+4x+|a-1|=0有实根,
∴△=16-4(|a-1|)≥0,
即-3≤a≤5,
故答案为:[-3,5].
B:∵AD为⊙O的切线,∴∠BAE=∠C,
∵AE平分∠CAB,∴∠BAC=2∠BAE,
又∵∠C+∠BAC=90°,∴∠BAE=∠C=30°.
则有BE=1,AB=

,BC=3,
∴AC=2

.
故答案为:2

.
C:l的直角坐标方程为 x+2y-1-2

=0,
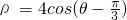
的直角坐标方程为
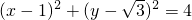
,
所以圆心

到直线l的距离

,
说明直线经过圆心,
∴|AB|=4.
故答案为:4.
点评:本题考查直线的参数方程、圆的极坐标方程、与圆有关的比例线段、绝对值不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想,此题应用弦切角、解直角三角形的知识,为基础题型.

 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)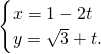 (t为参数)与圆
(t为参数)与圆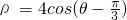 相交于A、B两点,则|AB|=________.
相交于A、B两点,则|AB|=________. 4
4 即-3≤a≤5,
即-3≤a≤5, ,BC=3,
,BC=3, .
. .
. =0,
=0,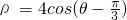 的直角坐标方程为
的直角坐标方程为 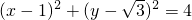 ,
, 到直线l的距离
到直线l的距离 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案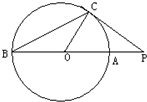 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)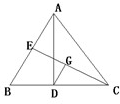 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)