
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.分析 (1)由题意可得c=1,运用椭圆的定义可得2a=4,a=2,再由椭圆的a,b,c的关系,可得b,进而得到椭圆方程;
(2)讨论当BC垂直于x轴,求得B,C的坐标,由共线求得P,Q的坐标,向量FP,FQ的坐标,由垂直的条件可得数量积为0,解得m=4,再考虑BC不垂直于x轴,设出直线方程,联立椭圆方程,运用韦达定理,结合三点共线,可得P,Q的纵坐标,再由向量垂直的条件,得到方程,解得m=4.
解答 解:(1)右焦点为F(1,0),可得
c=1,左焦点F'为(-1,0),
由椭圆的定义可得2a=|DF|+|DF'|
=$\frac{3}{2}$+$\sqrt{{2}^{2}+\frac{9}{4}}$=4,
即有a=2,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
则椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)当BC垂直于x轴,即有B(1,-$\frac{3}{2}$),C(1,$\frac{3}{2}$),
设P(m,s),Q(m,t),A(2,0),F(1,0),
由B,A,P共线,可得kAB=kAP,
即为$\frac{3}{2}$=$\frac{s}{m-2}$,即有s=$\frac{3}{2}$(m-2),
即有P(m,$\frac{3}{2}$(m-2)),$\overrightarrow{FP}$=(m-1,$\frac{3}{2}$(m-2)),
同样可得Q(m,-$\frac{3}{2}$(m-2)),$\overrightarrow{FQ}$=(m-1,-$\frac{3}{2}$(m-2)),
FP⊥FQ即为$\overrightarrow{FP}•\overrightarrow{FQ}$=0,
即有(m-1)2-$\frac{9}{4}$(m-2)2=0,
解得m=4;
当直线CB与x轴不垂直,则设直线CB的斜率为k,(k≠0)
∴直线CB的方程为y=k(x-1),k≠0,
又设B(x1,y1),C(x2,y2),P(m,y3),Q(m,y4),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,消y得(3+4k2)x2-8k2x+4k2-12=0,
∴x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
∴y1y2=k2(x1-1)(x2-1)=$\frac{-9{k}^{2}}{3+4{k}^{2}}$,
又∵A、B、P三点共线,
∴y3=(m-2)•$\frac{{y}_{1}}{{x}_{1}-2}$,同理y4=(m-2)•$\frac{{y}_{2}}{{x}_{2}-2}$,
∴$\overrightarrow{FP}$=(m-1,(m-2)•$\frac{{y}_{1}}{{x}_{1}-2}$),$\overrightarrow{FQ}$=(m-1,(m-2)•$\frac{{y}_{2}}{{x}_{2}-2}$),
由于$\overrightarrow{FP}•\overrightarrow{FQ}$=0,即为$\overrightarrow{FP}•\overrightarrow{FQ}$=(m-1)2+(m-2)2•$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}-2({x}_{1}+{x}_{2})+4}$=0,
分别代入x1+x2,x1x2,y1y2,可得(m-1)2-$\frac{9}{4}$(m-2)2=0,
解得m=4.
综上可得m=4.
点评 本题考查椭圆方程的求法和椭圆的性质,考查向量垂直的条件即为向量的数量积为0,解题时要认真审题,注意分类讨论思想的合理运用和化简整理的运算能力.


科目:高中数学 来源:2016-2017学年安徽六安一中高二上理周末检测三数学试卷(解析版) 题型:选择题
若数列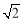 ,
, ,
, ,
, ,
, ,……,则
,……,则 是这个数列的第( )项
是这个数列的第( )项
A.8 B.9 C.10 D.11
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋$\frac{2π}{3}$到OD,连PD交圆O于点E,则PE=$\frac{3\sqrt{7}}{7}$.
如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋$\frac{2π}{3}$到OD,连PD交圆O于点E,则PE=$\frac{3\sqrt{7}}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com