
分析 a1=1,an=an-1+$\frac{1}{n(n-1)}$(n≥2),可得a2=a1+$\frac{1}{2}$=$\frac{3}{2}$,同理可得:a3,a4,a5.由an=an-1+$\frac{1}{n(n-1)}$,可得an-an-1=$\frac{1}{n-1}-\frac{1}{n}$,利用“裂项求和”方法即可得出.
解答 解:∵a1=1,an=an-1+$\frac{1}{n(n-1)}$(n≥2),∴a2=a1+$\frac{1}{2}$=$\frac{3}{2}$,同理可得:a3=$\frac{5}{3}$,a4=$\frac{7}{4}$,a5=$\frac{9}{5}$.
∵an=an-1+$\frac{1}{n(n-1)}$,∴an-an-1=$\frac{1}{n-1}-\frac{1}{n}$,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=$(\frac{1}{n-1}-\frac{1}{n})$+$(\frac{1}{n-2}-\frac{1}{n-1})$+…+$(1-\frac{1}{2})$+1=1-$\frac{1}{n}$+1=2-$\frac{1}{n}$,
点评 本题考查了数列递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为 ( )
A.2,4,6, 8 B.2,6,10,14
C.5,8,11,14 D.5,10,15,20
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:选择题
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且 =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且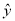 =-3.476x+5.648;③y与x正相关且
=-3.476x+5.648;③y与x正相关且 =5.437x+8.493;④y与x正相关且
=5.437x+8.493;④y与x正相关且 =-4.326x-4.578.其中一定不正确的结论的序号是( )
=-4.326x-4.578.其中一定不正确的结论的序号是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:填空题
下列各式:
(1) ;
;
(2)已知 ,则
,则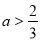 ;
;
(3)函数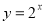 的图象与函数
的图象与函数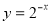 的图象关于y轴对称;
的图象关于y轴对称;
(4)函数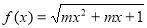 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是 ;
;
(5)函数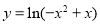 的递增区间为
的递增区间为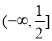 .
.
正确的有 .(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$ | B. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$ | C. | y=$\sqrt{2}$x-$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ | D. | y=$\sqrt{2}$x+$\frac{\sqrt{2}π}{4}$+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com