
分析 求得函数f(x)=a+$\frac{3}{x-b}$的反函数,与f-1(x)=1+$\frac{c}{2x+1}$对比,即可求得a,b和c的值.
解答 解:令y=f(x)=a+$\frac{3}{x-b}$,则x=b+$\frac{3}{y-a}$,
函数y=f(x)=a+$\frac{3}{x-b}$的反函数是:x=b+$\frac{3}{y-a}$=b+$\frac{6}{2y-2a}$,
函数f-1(x)=1+$\frac{c}{2x+1}$,对应比较,得 b=1,c=6,a=-$\frac{1}{2}$,
常数a、b、c的值-$\frac{1}{2}$,1,6.
点评 本题考查反函数的求法,考查转化思想,属于基础题.


科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:选择题
已知点A(1,3),B(4,-1),则与向量 同方向的单位向量为( )
同方向的单位向量为( )
A. B.
B.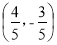 C.
C.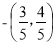 D.
D.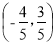
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
已知集合A={2,3},B={x|mx﹣6=0},若B⊆A,则实数m=( )
A.3 B.2
C.2或3 D.0或2或3
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
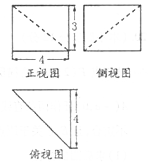
| A. | $\frac{\sqrt{34}}{2}$ | B. | $\frac{\sqrt{41}}{2}$ | C. | 17 | D. | 41 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
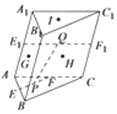 如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )
如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )| A. | 只可能经过点I | B. | 只可能经过点G,H | ||
| C. | 可能经过点G,H,I | D. | 不可能经过点G,H,I |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com