
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 的周长为12.
的周长为12.
(1)求点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)已知点![]() ,是否存在过点
,是否存在过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
【答案】(1)![]() ;(2)不存在,答案见解析.
;(2)不存在,答案见解析.
【解析】
(1)依题意根据椭圆的定义可知点![]() 的轨迹为椭圆,(除去与x轴的交点),
的轨迹为椭圆,(除去与x轴的交点),
设方程为![]() ,由
,由![]() ,
,![]() ,求出
,求出![]() 即可得到椭圆方程;
即可得到椭圆方程;
(2显然直线![]() 的斜率不存在时,直线与椭圆无交点;当直线
的斜率不存在时,直线与椭圆无交点;当直线![]() 的斜率存在时,设方程为
的斜率存在时,设方程为![]() ,联立直线与椭圆方程,消元,由
,联立直线与椭圆方程,消元,由![]() 求出
求出![]() 的取值范围,设点
的取值范围,设点![]() ,
,![]() 的中点
的中点![]() ,列出韦达定理,表示出
,列出韦达定理,表示出![]() ,由又
,由又![]() ,得到
,得到![]() ,得到方程判断方程的解即可;
,得到方程判断方程的解即可;
解:(1)由题意可得![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() 的周长为12,
的周长为12,
∴![]() ,
,
∴点P的轨迹是椭圆(除去与x轴的交点),
设方程为![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴点![]() 的轨迹C的方程为
的轨迹C的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,直线与椭圆无交点;
的斜率不存在时,直线与椭圆无交点;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的斜率为k,
的斜率为k,
则![]() ,
,
联立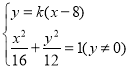 ,
,
得![]() ,
,
由![]() ,
,
解得![]() ,且
,且![]() .
.
设点![]() ,
,![]() 的中点
的中点![]()
∵![]() ,∴
,∴![]()
![]()
又∵![]() ,∴
,∴![]() ,
,
∵![]()
∴![]() ,此方程无解.
,此方程无解.
综上所述,不存在直线![]() 使得
使得![]() .
.


科目:高中数学 来源: 题型:
【题目】对一个量用两种方法分别算一次,由结果相同而构造等式,这种方法称为“算两次”的思想方法.利用这种方法,结合二项式定理,可以得到很多有趣的组合恒等式.
(1)根据恒等式![]() 两边
两边![]() 的系数相同直接写出一个恒等式,其中
的系数相同直接写出一个恒等式,其中![]() ;
;
(2)设![]() ,利用上述恒等式证明:
,利用上述恒等式证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆C:![]() 的左、右焦点,椭圆C过点M
的左、右焦点,椭圆C过点M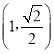 ,且MF2⊥F1F2.
,且MF2⊥F1F2.
(1)求椭圆C的方程;
(2)经过点P(2,0)的直线交椭圆C于A,B两点,若存在点Q(m,0),使得|QA|=|QB|.
①求实数m的取值范围:
②若线段F1A的垂直平分线过点Q,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月12日,国务院新闻办公室发布会重点介绍了改革开放40年,特别是党的十八大以来我国脱贫攻坚、精准扶贫取得的显著成绩,这些成绩为全面脱贫初步建成小康社会奠定了坚实的基础.下图是统计局公布的2010年~2019年年底的贫困人口和贫困发生率统计表.则下面结论正确的是( )
(年底贫困人口的线性回归方程为![]() (其中
(其中![]() 年份-2019),贫困发生率的线性回归方程为
年份-2019),贫困发生率的线性回归方程为![]() (其中
(其中![]() 年份-2009))
年份-2009))

A.2010年~2019年十年间脱贫人口逐年减少,贫困发生率逐年下降
B.2012年~2019年连续八年每年减贫超过1000万,且2019年贫困发生率最低
C.2010年~2019年十年间超过1.65亿人脱贫,其中2015年贫困发生率低于6%
D.根据图中趋势线可以预测,到2020年底我国将实现全面脱贫
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国大力发展新能源汽车工业,新能源汽车(含电动汽车)销量已跃居全球首位.某电动汽车厂新开发了一款电动汽车.并对该电动汽车的电池使用情况进行了测试,其中剩余电量y与行驶时问![]() (单位:小时)的测试数据如下表:
(单位:小时)的测试数据如下表:

(1)根据电池放电的特点,剩余电量y与行驶时间![]() 之间满足经验关系式:
之间满足经验关系式:![]() ,通过散点图可以发现y与
,通过散点图可以发现y与![]() 之间具有相关性.设
之间具有相关性.设![]() ,利用表格中的前8组数据求相关系数r,并判断是否有99%的把握认为
,利用表格中的前8组数据求相关系数r,并判断是否有99%的把握认为![]() 与
与![]() 之间具有线性相关关系;(当相关系数r满足
之间具有线性相关关系;(当相关系数r满足![]() 时,则认为有99%的把握认为两个变量具有线性相关关系)
时,则认为有99%的把握认为两个变量具有线性相关关系)
(2)利用![]() 与
与![]() 的相关性及表格中前8组数据求出
的相关性及表格中前8组数据求出![]() 与
与![]() 之间的回归方程;(结果保留两位小数)
之间的回归方程;(结果保留两位小数)
(3)如果剩余电量不足0.8,电池就需要充电.从表格中的10组数据中随机选出8组,设X表示需要充电的数据组数,求X的分布列及数学期望.
附:相关数据:![]() .
.
表格中前8组数据的一些相关量:![]() ,
,![]() ,
,
相关公式:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和戗距的最小二乘估计公式分别为:
的斜率和戗距的最小二乘估计公式分别为: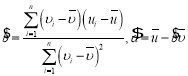 ,
,
相关系数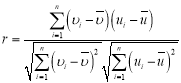 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的参数方程为
的参数方程为 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到![]() 距离的最大值及该点坐标.
距离的最大值及该点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com