
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数.
的导函数.
(1)若![]() ,当
,当![]() 时,函数
时,函数![]() 在
在![]() 内有唯一的极大值,求
内有唯一的极大值,求![]() 的取值范围;
的取值范围;
(2)若![]() ,
,![]() ,试研究
,试研究![]() 的零点个数.
的零点个数.
【答案】(1)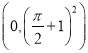 ;(2)
;(2)![]() 有
有![]() 个零点
个零点
【解析】
(1)先求导得![]() ,再分
,再分![]() 和
和![]() 两种情况讨论求得
两种情况讨论求得![]() 的取值范围;(2)分析可知,只需研究
的取值范围;(2)分析可知,只需研究![]() 时零点的个数情况,再分
时零点的个数情况,再分![]() 两种情形讨论即可.
两种情形讨论即可.
(1)当![]() 时,
时,![]() ,
,![]() ,
,![]()
![]() 在
在![]() 是减函数,且
是减函数,且![]() ,
,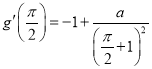 ,
,
①,当![]() ,
,![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 是增函数,无极值;
是增函数,无极值;
②,当![]() ,
,![]() 时,
时,![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,
,![]() 单调递增;
单调递增;
![]() ,
,![]() ,
,![]() 单调递减,
单调递减,![]() 为
为![]() 唯一的极大值点,所以
唯一的极大值点,所以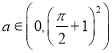
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,可知,
,可知,
(i)![]() 时,
时,![]() ,无零点;所以只需研究
,无零点;所以只需研究![]() ,
,![]() ,
,
(ii)![]() 时,
时,![]() ,可知
,可知![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,![]() 唯一的
唯一的![]() ,
,![]() ;
;
(iii)当![]() ,
,![]() 是减函数,且
是减函数,且![]() ,
,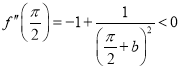 ,
,
则![]() ,
,![]() ,
,![]() 在
在![]() 是增函数,
是增函数,![]() 是减函数,并且
是减函数,并且![]() ,
,![]() ,
,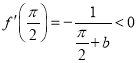 ,
,
所以![]() ,
,![]() ;
;![]() ,
,![]() ,且知
,且知![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 单调递减.
单调递减.
又因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
![]() ,
,![]() ,综上所述,由(i)(ii)(iii)可知,
,综上所述,由(i)(ii)(iii)可知,![]() 有
有![]() 个零点.
个零点.


科目:高中数学 来源: 题型:
【题目】某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km,![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短.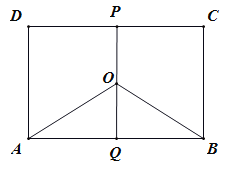
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为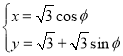 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,点
的交点,点![]() 是曲线
是曲线![]() 与
与![]() 的交点,
的交点,![]() 、
、![]() 均异于原点
均异于原点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 的周长为12.
的周长为12.
(1)求点![]() 的轨迹
的轨迹![]() 的方程.
的方程.
(2)已知点![]() ,是否存在过点
,是否存在过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com