
【题目】如图,三棱柱![]() 中,底面
中,底面![]() 为等边三角形,E,F分别为
为等边三角形,E,F分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() .
.
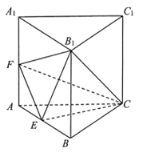
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)通过计算可得![]() ,通过证明
,通过证明![]() 平面
平面![]() ,可得
,可得![]() ,再根据直线与平面垂直的判定定理可得
,再根据直线与平面垂直的判定定理可得![]() 平面
平面![]() ;
;
(2)先说明直线![]() ,
,![]() ,
,![]() 两两垂直,再以
两两垂直,再以![]() ,
,![]() ,
,![]() 的方向为x,y,z轴的正方向,以点E为原点,建立空间直角坐标系,然后利用空间向量可求得结果.
的方向为x,y,z轴的正方向,以点E为原点,建立空间直角坐标系,然后利用空间向量可求得结果.
(1)证明:设![]() ,∵
,∵![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∵点E为棱![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵三棱柱![]() 的侧面
的侧面![]() 为平行四边形,
为平行四边形,
∴四边形![]() 为矩形,
为矩形,
∵点F为棱![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵三棱柱的底面![]() 是正三角形,E为
是正三角形,E为![]() 的中点,
的中点,
∴![]() .
.
∵![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() 相交,
相交,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)可知![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴三棱柱![]() 是正三棱柱,
是正三棱柱,
设![]() 的中点为M,则直线
的中点为M,则直线![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
分别以![]() ,
,![]() ,
,![]() 的方向为x,y,z轴的正方向,以点E为原点,建立如图所示的空间直角坐标系,
的方向为x,y,z轴的正方向,以点E为原点,建立如图所示的空间直角坐标系,
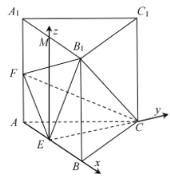
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则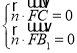 ,则
,则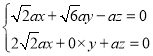 ,则
,则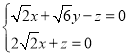 ,
,
不妨取![]() ,则
,则![]() ,则
,则![]() ,所以
,所以![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则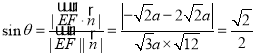 ,
,
因为![]() ,所以
,所以![]()
则直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某疫苗进行安全性临床试验.该疫苗安全性的一个重要指标是:注射疫苗后人体血液中的高铁血红蛋白(MetHb)的含量(以下简称为“M含量”)不超过1%,则为阴性,认为受试者没有出现高铁血红蛋白血症(简称血症);若M含量超过1%,则为阳性,认为受试者出现血症.若一批受试者的M含量平均数不超过0.65%,且出现血症的被测试者的比例不超过5%,则认为该疫苗在M含量指标上是“安全的”;否则为“不安全”.现有男、女志愿者各200名接受了该疫苗注射,按照性别分层,随机抽取50名志愿者进行M含量的检测,其中女性志愿者被检测出阳性的恰好1人.经数据整理,制得频率分布直方图如下.(注:在频率分布直方图中,同一组数据用该区间的中点值作代表.)
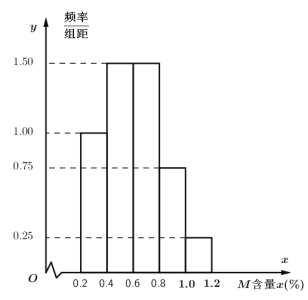
(1)请说明该疫苗在M含量指标上的安全性;
(2)请利用样本估计总体的思想,完成这400名志愿者的![]() 列联表,并判断是否有超过99%的把握认为,注射疫苗后,高铁血红蛋白血症与性别有关?
列联表,并判断是否有超过99%的把握认为,注射疫苗后,高铁血红蛋白血症与性别有关?
男 | 女 | |
阳性 | ||
阴性 |
附: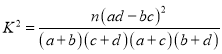 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩共分五组,得到如下的频率分布表:
名学生的笔试成绩,按成绩共分五组,得到如下的频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
(1)请写出频率分布表中![]() 、
、![]() 、
、![]() 的值,若同组中的每个数据用该组区间的中间值代替,请估计全体考生的平均成绩;
的值,若同组中的每个数据用该组区间的中间值代替,请估计全体考生的平均成绩;
(2)为了能选出最优秀的学生,高校决定在笔试成绩高的第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名考生进入第二轮面试,求第
名考生进入第二轮面试,求第![]() 、
、![]() 、
、![]() 组中每组各抽取多少名考生进入第二轮的面试;
组中每组各抽取多少名考生进入第二轮的面试;
(3)在(2)的前提下,学校要求每个学生需从![]() 、
、![]() 两个问题中任选一题作为面试题目,求第三组和第五组中恰好有
两个问题中任选一题作为面试题目,求第三组和第五组中恰好有![]() 个学生选到问题
个学生选到问题![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一个量用两种方法分别算一次,由结果相同而构造等式,这种方法称为“算两次”的思想方法.利用这种方法,结合二项式定理,可以得到很多有趣的组合恒等式.
(1)根据恒等式![]() 两边
两边![]() 的系数相同直接写出一个恒等式,其中
的系数相同直接写出一个恒等式,其中![]() ;
;
(2)设![]() ,利用上述恒等式证明:
,利用上述恒等式证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com