
【题目】已知函数![]() ,
,![]() .
.
(1)若直线![]() 与函数
与函数![]() 的图象相切,求实数
的图象相切,求实数![]() 的值;
的值;
(2)若存在![]() ,
,![]() ,使
,使![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)由f′(x0)![]() .可得切线方程为:y=(
.可得切线方程为:y=(![]() )x+lnx0,与直线y=2x完全相同,可得
)x+lnx0,与直线y=2x完全相同,可得![]() =2,lnx0=0.即可得出a.
=2,lnx0=0.即可得出a.
(2)设t(x)=ex﹣x,x∈R.t′(x)=ex﹣1,利用导数研究其单调性可得0是函数t(x)的极小值点,可得![]() .再由g(x2)=0,解得x2,可得x1的范围.从而问题可转化为函数f(x)=lnx﹣ax+1在x∈(1,+∞)上有零点.由f′(x)
.再由g(x2)=0,解得x2,可得x1的范围.从而问题可转化为函数f(x)=lnx﹣ax+1在x∈(1,+∞)上有零点.由f′(x)![]() a
a![]() .对a分类讨论,研究其单调性即可得出.
.对a分类讨论,研究其单调性即可得出.
(3)构造函数F(x)=x2+g(x)﹣f(x),利用导数研究其单调性极值与最值即可得出.
(1)设切点坐标为![]() ,
,
由![]() ,得
,得![]() ,
,
所以切线方程为:![]() ,
,
即![]() .
.
因为直线![]() 与函数
与函数![]() 的图象相切,
的图象相切,
所以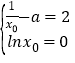 ,解得
,解得![]() .
.
(2)设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,
,
且当![]() 时,
时,![]() :当
:当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在
在![]() 时取得极小值为0,即
时取得极小值为0,即![]() .
.
由![]() ,可得
,可得![]() ,
,
所以![]() 即为
即为![]() ,
,
由题意可得:函数![]() 在
在![]() 上有零点.
上有零点.
因为![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,函数
,函数![]() 在
在![]() 上无零点:
上无零点:
当![]() 时,令
时,令![]() ,得
,得![]() .
.
①若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
所以函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,函数
,函数![]() 在
在![]() 上无零点:
上无零点:
②若![]() ,即
,即![]() 时,
时,
当![]() 时,
时,![]() :当
:当![]() 时,
时,![]() .
.
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,
,
因为![]() ,所以函数
,所以函数![]() 在
在![]() 上无零点:
上无零点:
又![]() ,
,
令![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,
,
所以![]() ,且
,且![]() 在
在![]() 的图象连续不断,
的图象连续不断,
所以函数![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
即函数![]() 在
在![]() 上有零点.
上有零点.
综上所述,![]() .
.
(3)当![]() 时,
时,![]() ,
,
令![]()
![]() ,
,
则![]() ,
,
令![]() ,则当
,则当![]() 时,
时,![]() ,
,
所以函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
又![]() ,
,![]() ,
,
所以函数![]() 存在唯一的零点
存在唯一的零点![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
故![]() ,
,
由![]() 得:
得:![]() ,
,
两边取对数得:![]() ,故
,故![]() ,
,
所以![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】过直线2x+y+4=0和圆x2+y2+2x﹣4y+1=0的交点,且面积最小的圆方程为( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左.右顶点分别为A,B,离心率为
(a>b>0)的左.右顶点分别为A,B,离心率为![]() ,点P
,点P![]() 为椭圆上一点.
为椭圆上一点.
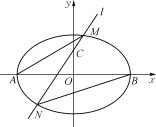
(1) 求椭圆C的标准方程;
(2) 如图,过点C(0,1)且斜率大于1的直线l与椭圆交于M,N两点,记直线AM的斜率为k1,直线BN的斜率为k2,若k1=2k2,求直线l斜率的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是圆
是圆![]() :
:![]() 上的动点,定点
上的动点,定点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,记
,记![]() 点的轨迹为
点的轨迹为![]() .
.
(Ⅰ)求轨迹![]() 的方程;
的方程;
(Ⅱ)若动直线![]() :
:![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,点
,点![]() 在轨迹
在轨迹![]() 上,且四边形
上,且四边形![]() 为平行四边形.证明:四边形
为平行四边形.证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
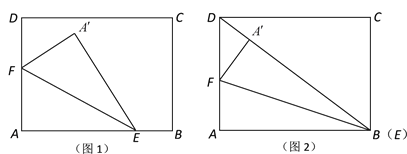
【题目】南通风筝是江苏传统手工艺品之一.现用一张长2 m,宽1.5 m的长方形牛皮纸ABCD裁剪风筝面,裁剪方法如下:分别在边AB,AD上取点E,F,将三角形AEF沿直线EF翻折到![]() 处,点
处,点![]() 落在牛皮纸上,沿
落在牛皮纸上,沿![]() ,
,![]() 裁剪并展开,得到风筝面
裁剪并展开,得到风筝面![]() ,如图1.
,如图1.
(1)若点E恰好与点B重合,且点![]() 在BD上,如图2,求风筝面
在BD上,如图2,求风筝面![]() 的面积;
的面积;
(2)当风筝面![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 到AB距离的最大值.
到AB距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,先求出![]() 关于
关于![]() 的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过
的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过![]() ,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的回归关系,如果该种机器配件的成本是![]() 元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: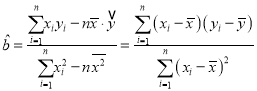 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区![]() 年该农产品的产量;
年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 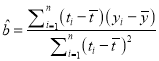 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com