
已知椭圆:()过点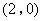 ,且椭圆的离心率为.
,且椭圆的离心率为.
(Ⅰ)求椭圆的方程;
(Ⅱ)若动点在直线上,过作直线交椭圆于两点,且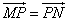 ,再过作直线.证明:直线恒过定点,并求出该定点的坐标.
,再过作直线.证明:直线恒过定点,并求出该定点的坐标.
科目:高中数学 来源: 题型:
在边长为2的正方形 中有一个不规则的图形
中有一个不规则的图形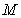 ,用随机模拟方法来估计不规则图形的面积.若在正方形
,用随机模拟方法来估计不规则图形的面积.若在正方形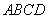 中随机产生了
中随机产生了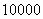 个点,落在不规则图形
个点,落在不规则图形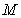 内的点数恰有2000个,则在这次模拟中,不规则图形
内的点数恰有2000个,则在这次模拟中,不规则图形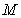 的面积的估计值为__________.
的面积的估计值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知四边形是边长为的正方形,且平面,为上动点,过且垂直于的平面交于,那么异面直线 与
与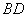 所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥
所成的角的度数为 ,当三棱锥的体积取得最大值时, 四棱锥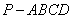 的高
的高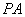 的长为 .
的长为 .
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
有20位同学,编号从1至20,现在从中抽取4人作问卷调查,若用系统抽样方法,则所抽取的编号可能是
A. 2,4,6,8 B. 2,6,10,14 C. 2,7,12,17 D. 5,8,9,14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com