解:(1)因为6a
3=8a
1+a
5,所以6q
2=8+q
4,
解得q
2=4或q
2=2(舍),则q=2
又a
1=2,所以a
n=2
n(2)由2n
2-(t+b
n)n+

b
n=0,得b
n=

,
所以b
1=2t-4,b
2=16-4t,b
3=12-2t,
则由b
1+b
3=2b
2,得t=3
而当t=3时,b
n=2n,由b
n+1-b
n=2(常数)知此时数列{b
n}为等差数列;
(3)因为c
1=c
2=c
3=2,易知m=1不合题意,m=2适合题意
当m≥3时,若后添入的数2等于c
m+1个,则一定不适合题意,
从而c
m+1必是数列{a
n}中的某一项a
k+1,
则(2+2
2+2
3+…+2
k)+2(b
1+b
2+b
3+…+b
k)=2×2
k+1,
即
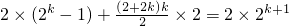
,即2
k+1-2k
2-2k+2=0.
也就是2
k=k
2+k-1,
易证k=1,2,3,4不是该方程的解,而当n≥5时,2
n>n
2+n-1成立,证明如下:
1°当n=5时,2
5=32,k
2+k-1=29,左边>右边成立;
2°假设n=k时,2
k>k
2+k-1成立,
当n=k+1时,2
k+1>2k
2+2k-2=(k+1)
2+(k+1)-1+k
2-k-3
≥(k+1)
2+(k+1)-1+5k-k-3=(k+1)
2+(k+1)-1+k+3(k-1)>(k+1)
2+(k+1)-1
这就是说,当n=k+1时,结论成立.
由1°,2°可知,2
n>n
2+n-1(n≥5)时恒成立,故2
k=k
2+k-1无正整数解.
综上可知,满足题意的正整数仅有m=2.
分析:(1)由3a
3是8a
1与a
5的等差中项得到6a
3=8a
1+a
5,根据首项2和公比q,利用等比数列的通项公式化简这个式子即可求出q的值,利用首项和公比即可得到通项公式;
(2)由2n
2-(t+b
n)n+

b
n=0解出b
n,列举出b
1,b
2和b
3,要使数列{b
n}为等差数列,根据等差数列的性质可知b
1+b
3=2b
2,把b
1,b
2和b
3的值代入即可求出t的值;
(3)显然c
1=c
2=c
3=2,容易判断m=1时不合题意,m=2适合题意,当m大于等于3时,得到c
m+1必是数列{a
n}中的某一项a
k+1,然后根据T
n=2c
m+1列举出各项,利用等差、等比数列的求和公式化简后得到2
k=k
2+k-1,把k=1,2,3,4,代入等式得到不是等式的解,利用数学归纳法证明得到k大于等于5时方程没有正整数解,所以得到满足题意的m仅有一个解m=2.
点评:此题考查学生灵活运用等差数列的性质及等比数列的通项公式化简求值,灵活运用数列解决实际问题,以及会利用数学归纳法进行证明,是一道比较难的题.

 bn=0(t∈R,n∈N*).
bn=0(t∈R,n∈N*). bn=0,得bn=
bn=0,得bn= ,
,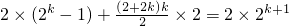 ,即2k+1-2k2-2k+2=0.
,即2k+1-2k2-2k+2=0. bn=0解出bn,列举出b1,b2和b3,要使数列{bn}为等差数列,根据等差数列的性质可知b1+b3=2b2,把b1,b2和b3的值代入即可求出t的值;
bn=0解出bn,列举出b1,b2和b3,要使数列{bn}为等差数列,根据等差数列的性质可知b1+b3=2b2,把b1,b2和b3的值代入即可求出t的值;

 阅读快车系列答案
阅读快车系列答案