
分析 (Ⅰ)m=1时,可求f'(x),f''(x),令f''(x)=0,得x=0,可得当x≥0时,f''(x)≥0,从而得证;
(Ⅱ)由(Ⅰ)和(2)式知,当x≤0时,f''(x)≤0,可得 对?x∈R,f'(x)≥0,即ex≥x+1,分类讨论当x≥-1时,当x<-1时,函数y=f(x)的零点个数即可得解.
解答 (本题满分为12分)
解:(Ⅰ)m=1时,$f(x)={e^x}-\frac{x^2}{2}-x-1$,则f'(x)=ex-x-1,…(1)
则f''(x)=ex-1,…(2),
令f''(x)=0,得x=0,
当x≥0时,ex≥1,
∴ex-1≥0,即f''(x)≥0,
∴函数y=f'(x)在[0,+∞)上为增函数,即当x≥0时,f′(x)≥f′(0)=0,
∴函数y=f(x)在[0,+∞)上为增函数,即当x≥0时f(x)≥f(0)=0.…(5分)
(Ⅱ)由(Ⅰ)和(2)式知,当x≤0时,ex-1≤0,
∴f''(x)≤0,
∴函数f'(x)=ex-x-1的减区间为(-∞,0],增区间为(0,+∞),
∴f'(x)min=f'(0)=0,
∴对?x∈R,f'(x)≥0,即ex≥x+1,…(3)
①当x≥-1时,x+1≥0,又m≤1,
∴m(x+1)≤x+1,
∴由(3)得ex-m(x+1)≥ex-(x+1)≥0,即f'(x)≥0,
∴函数y=f(x)x≥-1为增函数,又f(0)=0,
∴当x>0时,f(x)>f(0)=0,当-1≤x<0时,f(x)<f(0)=0,
∴函数y=f(x)在x≥-1时有且仅有一个零点x=0,
②当x<-1时,
ⅰ)当0≤m≤1时,-m(x+1)≥0,ex>0,
∴f'(x)=ex-m(x-1)>0,
∴函数y=f(x)在x<-1时递减,
∴$f(x)<f({-1})={e^{-1}}+\frac{m}{2}-1<\frac{m-1}{2}<0$,
故0≤m≤1时,函数y=f(x)在x<-1时无零点,
ⅱ)当m<0时,由f'(x)=ex-mx-m,得f''(x)=ex-m>0,
∴函数y=f'(x)在x<-1时递增,f'(-1)=e-1>0,
当$x≤\frac{{{e^{-1}}}}{m}-1$时,f'(x)<e-1-m(x+1)≤0,
∴由函数零点定理知$?{x^*}∈({\frac{{{e^{-1}}}}{m}-1,-1})$,使f'(x*)=0,
故当x∈(x*,-1)时,0=f'(x*)<f'(x)<f'(-1)=e-1,
当x∈(-∞,x*)时,f'(x)<f'(x*)=0,
∴函数y=f(x)的减区间为(-∞,x*),增区间为(x*,-1),
又$f({-1})={e^{-1}}+\frac{m}{2}-1<0$,
∴对?x∈[x*,-1),f(x)<0,
又当$x<-\sqrt{1-\frac{2}{m}}-1({x<-1})$时,$-\frac{m}{2}{x^2}-mx-1>0$,
∴f(x)>0,
由f(x*)<0,
∴$({-\sqrt{1-\frac{2}{m}},-1})⊆$(-∞,x*),
再由函数零点定理知?${x_0}∈({-∞,{x^*}})$,使得f(x0)=0,
综上所述:当0≤m≤1时,函数y=f(x)有且仅有一个零点,
当m<0时,函数y=f(x)有两个零点. …(12分)
点评 本题主要考查利用导数研究函数的单调性,函数零点的判定定理的应用,考查学生运用分类讨论思想、划归思想解决数学问题的能力,属难题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为π | |
| B. | 直线x=$\frac{π}{12}$是函数f(x)图象的对称轴 | |
| C. | 函数f(x)的图象关于点(-$\frac{π}{6}$,0)对称 | |
| D. | 函数f(x)在区间(-$\frac{π}{12}$,$\frac{5π}{12}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
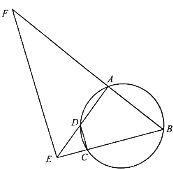 如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.
如图,圆内接四边形ABCD的边BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com