
分析 (Ⅰ)由题意和内角和定理求出C,由两角差的余弦公式、两角和的正弦公式化简已知的等式,由A的范围和特殊角的三角函数值求出A,判断出△ABC的形状,由勾股定理求出c;
(Ⅱ)利用二倍角公式及变形,两角和的正弦公式化简f(A),由A的范围和正弦函数的图象与性质,求出
f(A)的取值范围.
解答 解:(Ⅰ)∵B=45°,∴C=180°-A-B=135°-A,
∴${cosC}+\sqrt{2}{cosA}=cos({{{135}^0}-A})+\sqrt{2}{cosA}$
=$-\frac{{\sqrt{2}}}{2}{cosA}+\frac{{\sqrt{2}}}{2}sinA+\sqrt{2}{cosA}$
=$\frac{{\sqrt{2}}}{2}sinA+\frac{{\sqrt{2}}}{2}{cosA}=sin({A+{{45}^0}})=1$,
又∵A+450∈(450,1800),∴A+450=900,得A=45°.
∴△ABC为等腰直角三角形,$c=\sqrt{{a^2}+{b^2}}=3\sqrt{2}$.…(6分)
(Ⅱ)∵$\overrightarrow m$=(2sin$\frac{A}{2}$,-1),$\overrightarrow n$=($\sqrt{3}$cos$\frac{A}{2}$,2sin2$\frac{A}{2}}$),
∴$f(A)=\overrightarrow{m}•\overrightarrow{n}=2sin\frac{A}{2}•\sqrt{3}cos\frac{A}{2}-2si{n}^{2}\frac{A}{2}$
=$\sqrt{3}$sinA-(1-cosA)=$2sin(A+\frac{π}{6})-1$(10分)
由$0<A<\frac{3}{4}π$得,$\frac{π}{6}<A+\frac{π}{6}<\frac{11}{12}π$,
∴$\frac{\sqrt{6}-\sqrt{2}}{4}<sin(A+\frac{π}{6})≤1$,则$f(A)∈({\frac{{\sqrt{6}-\sqrt{2}-2}}{2},1}]$,
即f(A)的取值范围是$(\frac{\sqrt{6}-\sqrt{2}-2}{2},1]$ …(6分)
点评 本题考查了二倍角公式及变形,两角和的余弦公式、两角差的余弦公式,以及正弦函数的图象与性质,考查整体思想,化简、变形能力,注意内角的范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| 一个月内每天做题数x | 5 | 8 | 6 | 4 | 7 |
| 数学月考成绩y | 82 | 87 | 84 | 81 | 86 |
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
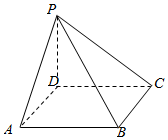 已知线段PD垂直于正方形ABCD所在平面,D为垂足,PD=3,AB=4,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,PD=3,AB=4,连接PA、PB、PC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
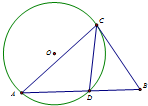 如图,弦CD平分∠ACB,BC切⊙O于点C,延长弦AD交BC于点B,若⊙O的半径长为$\frac{5}{2}$,CD=3,则AC=$\frac{24}{5}$,BD=$\frac{25}{13}$.
如图,弦CD平分∠ACB,BC切⊙O于点C,延长弦AD交BC于点B,若⊙O的半径长为$\frac{5}{2}$,CD=3,则AC=$\frac{24}{5}$,BD=$\frac{25}{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com