
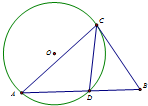
 如图,弦CD平分∠ACB,BC切⊙O于点C,延长弦AD交BC于点B,若⊙O的半径长为$\frac{5}{2}$,CD=3,则AC=$\frac{24}{5}$,BD=$\frac{25}{13}$.
如图,弦CD平分∠ACB,BC切⊙O于点C,延长弦AD交BC于点B,若⊙O的半径长为$\frac{5}{2}$,CD=3,则AC=$\frac{24}{5}$,BD=$\frac{25}{13}$. 分析 连接OC,OD,在等腰三角形COD中,运用余弦定理可得cos∠COD,由∠COD=2∠A,可得cosA,由等腰三角形可得AC=6cosA;在三角形BCD中,运用两角和的正弦公式,求得sinB,运用正弦定理可得BD.
解答 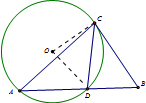 解:由弦CD平分∠ACB,可得∠ACD=∠BCD,
解:由弦CD平分∠ACB,可得∠ACD=∠BCD,
由弦切角定理,可得∠BCD=∠A,
即∠A=∠ACD,则AD=CD=3,
则AC=2ADcosA=6cosA,
连接OC,OD,即有∠COD=2∠A,
由⊙O的半径长为$\frac{5}{2}$,CD=3,
在等腰三角形COD中,cos∠COD=$\frac{\frac{25}{4}+\frac{25}{4}-9}{2×\frac{25}{4}×\frac{25}{4}}$=$\frac{7}{25}$,
可得2cos2A-1=$\frac{7}{25}$,解得cosA=$\frac{4}{5}$,
AC=6×$\frac{4}{5}$=$\frac{24}{5}$;
在△BCD中,CD=3,∠CDB=2∠A,∠BCD=∠A,
则cos∠CDB=cos∠COD=$\frac{7}{25}$,sin∠CDB=$\sqrt{1-(\frac{7}{25})^{2}}$=$\frac{24}{25}$,
sinB=sin(∠CDB+∠BCD)=sin∠CDBcos∠BCD+cos∠CDBsin∠BCD
=$\frac{24}{25}$×$\frac{4}{5}$+$\frac{7}{25}$×$\frac{3}{5}$=$\frac{117}{125}$,
由正弦定理可得$\frac{BD}{sin∠DCB}$=$\frac{DC}{sinB}$,
BD=$\frac{CDsin∠DCB}{sinB}$=$\frac{3×\frac{3}{5}}{\frac{117}{125}}$=$\frac{25}{13}$.
故答案为:$\frac{24}{5}$,$\frac{25}{13}$.
点评 本题考查圆的弦切角定理、三角形的内角和外角的关系、正弦定理和余弦定理的运用,考查推理和运算能力,属于中档题.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $12\sqrt{3}$ | B. | $12\sqrt{2}$ | C. | $100\sqrt{3}$ | D. | $100\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com