
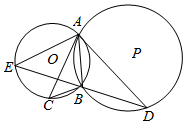
 如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.分析 (1)根据弦切角定理,得到∠BAP=∠C,结合PE平分∠APC,可得∠BAP+∠APD=∠C+∠CPE,最后用三角形的外角可得∠ADE=∠AED;
(2)通过内角相等证明出△APC∽△BPA,根据AC=AP得到∠APC=∠C,结合(I)中的结论可得∠APC=∠C=∠BAP,再在△APC中根据直径BC得到∠PAC=90°+∠BAP,利用三角形内角和定理可得∠C=∠APC=∠BAP=30°.利用直角三角形中正切的定义,得到$\frac{AC}{AB}$=$\sqrt{3}$,即可证明结论.
解答 证明:(1)∵PA是切线,AB是弦,∴∠BAP=∠C
又∵∠APD=∠CPE,∴∠BAP+∠APD=∠C+∠CPE
∵∠ADE=∠BAP+∠APD,∠AED=∠C+∠CPE
∴∠ADE=∠AED; …(5分)
(2)由(1)知∠BAP=∠C,又∠APC=∠BPA,∴△APC∽△BPA,
∴$\frac{PC}{PA}=\frac{AC}{AB}$,
∵AC=AP,∠BAP=∠C=∠APC,
由三角形的内角和定理知:∠C+∠APC+∠PAC=180°,
∵BC是圆O的直径,∴∠BAC=90°
∴∠C+∠APC+∠BAP=90°,∴∠C=∠APC=∠BAP=30°,
在Rt△ABC中,$\frac{AC}{AB}$=$\sqrt{3}$,∴$\frac{PC}{PA}$=$\sqrt{3}$,∴PC=$\sqrt{3}$PA …(10分)
点评 本题综合考查了弦切角、三角形的外角定理、直角三角形中三角函数的定义和相似三角形的性质等知识点,属于中档题.找到题中角的等量关系,计算出Rt△ABC是含有30度的直角三角形,是解决本题的关键所在.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
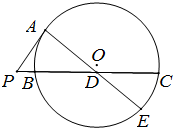 如图,P为⊙O外一点,PA是⊙O的切线,A为切点,割线PBC与⊙O相交于B,C两点,且PC=3PA,D为线段BC的中点,AD的延长线交⊙O于点E.若PB=1,则PA的长为3;AD•DE的值是16.
如图,P为⊙O外一点,PA是⊙O的切线,A为切点,割线PBC与⊙O相交于B,C两点,且PC=3PA,D为线段BC的中点,AD的延长线交⊙O于点E.若PB=1,则PA的长为3;AD•DE的值是16.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
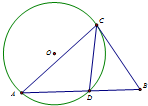 如图,弦CD平分∠ACB,BC切⊙O于点C,延长弦AD交BC于点B,若⊙O的半径长为$\frac{5}{2}$,CD=3,则AC=$\frac{24}{5}$,BD=$\frac{25}{13}$.
如图,弦CD平分∠ACB,BC切⊙O于点C,延长弦AD交BC于点B,若⊙O的半径长为$\frac{5}{2}$,CD=3,则AC=$\frac{24}{5}$,BD=$\frac{25}{13}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
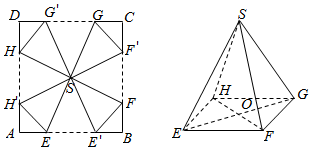 为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).
为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com