
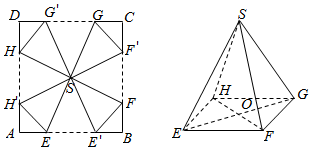
 为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).
为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).分析 (1)根据面面垂直的判定定理进行证明
(2)用正方形的面积减去4(S△EAH'+S△SEE'),即可得到四棱锥的侧面积,结合一元二次不等式进行求解即可.
(3)根据正四棱锥S-EFGH的外接球的性质求出外接球的半径进行求解即可.
解答 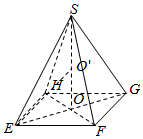 证明:∵折后A,B,C,D重合于一点O,
证明:∵折后A,B,C,D重合于一点O,
∴拼接成底面EFGH的四个直角三角形必为全等的等腰直角三角形,
∴底面EFGH是正方形,故EG⊥FH,
∵在原平面EFGH是正方形,故EG⊥FH,
∵在原平面图形中,等腰三角形△SEE′≌△SGG′,
∴SE=SG,∴EG⊥SO,
又∵SO、FH?平面SFH,SO∩FH=O,
∴EG⊥平面SFH,
又∵EG?平面SEC,∴平面SEG⊥平面SFH.
(2)∵AE=BE′=x(cm).
∴EE'=20-2x,有EE'>0得0<x<10,
则△SEE'的高为20,
则礼品袋的侧面积S=20×20-4(S△EAH'+S△SEE')
=400-4[($\frac{1}{2}$x2+$\frac{1}{2}$(20-2x)×10]=400-(2x2+400-40x)=-2x2+40x,
由S=-2x2+40x≥128得x2-20x+64≤0,得4≤x≤16,
∵0<x<10,∴4≤x<10.
(3)当x=5时,OE=OF=AE=5,则EF=5$\sqrt{2}$,包装盒的内径最小值,
即为正四棱锥S-EFGH的外接球的半径R,
设正四棱锥的外接球的球心为O',
则O'在正四棱锥S-EFGH的高SO上,连接EO',
则Rt△SEO中,SO=10,
∴O'E=R,O'O=10-R,
Rt△EOO'中,OE2+O'O2=O'E2,
∴52+(10-R)2=R2,
即25+100-20R=0,得R=$\frac{125}{20}=\frac{25}{4}$=6.25,
即包装盒的内径R的最小值是6.25.
点评 本题主要考查面面垂直的判断以及四棱锥外接球的性质,以及四棱锥侧面积的计算,利用函数思想是解决本题的关键.综合性较强,难度较大.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 阅读过莫言的 作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
| 男生 | 3 | 6 | 11 | 18 | 12 |
| 女生 | 4 | 8 | 13 | 15 | 10 |
| 非常了解 | 一般了解 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)≥0 | |
| B. | f(1)>f(14) | |
| C. | y=f(x)的解析式可能为y=2cos2$\frac{π}{6}$x | |
| D. | 若x2+y2=9与y=f(x)有且仅有三个交点,则在[0,3]上将y=f(x)的图象沿y轴旋转一周得到的几何体的体积为9π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|-$\sqrt{2}$≤a<-1} | B. | {a|-$\sqrt{2}$<a≤-1} | C. | {a|-$\sqrt{2}$<a<-1} | D. | {a|-$\sqrt{2}$≤a≤-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com