
分析 (1)当a=5代入求得g(x)的解析式,求出导数,求得g(1)和切线斜率k=g′(1),由直线方程的点斜式求得切线方程;
(2)把f(x)和g(x)的解析式代入g(x)=2exf(x)分离变量a,构造辅助函数,求得x∈[$\frac{1}{e}$,e]在的最大和最小值,即可求得实数a的取值范围.
解答 解:(1)当a=5,g(x)=(-x2+5x-3)ex,
g′(x)=(-x2+3x+2)ex,
∴在x=1处切线的斜率为k=g′(1)=4e.
g(1)=e,…(4分)
所以切线方程为:y-e=4e(x-1),即y-4ex+3e=0.…(6分)
(2)由g(x)=2exf(x),x∈[$\frac{1}{e}$,e]可得:2xlnx=-x2+ax-3,
a=x+2lnx+$\frac{3}{x}$,…(8分)
令h(x)=x+2lnx+$\frac{3}{x}$,h′(x)=1+$\frac{2}{x}$-$\frac{3}{{x}^{2}}$=$\frac{(x+3)(x-1)}{{x}^{2}}$.
| x | ($\frac{1}{e}$,1) | 1 | (1,e) |
| h′(x)= | - | 0 | + |
| h(x) | 单调递减 | 极小值(最小值) | 单调递增 |
点评 本题考查了导数在求函数最值中的应用,考查利用导函数求函数的单调性,构造辅助函数求含字母系数的范围问题,考查分析问题及解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
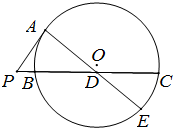 如图,P为⊙O外一点,PA是⊙O的切线,A为切点,割线PBC与⊙O相交于B,C两点,且PC=3PA,D为线段BC的中点,AD的延长线交⊙O于点E.若PB=1,则PA的长为3;AD•DE的值是16.
如图,P为⊙O外一点,PA是⊙O的切线,A为切点,割线PBC与⊙O相交于B,C两点,且PC=3PA,D为线段BC的中点,AD的延长线交⊙O于点E.若PB=1,则PA的长为3;AD•DE的值是16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
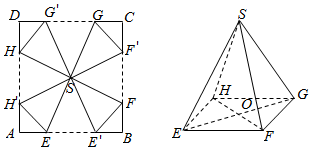 为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).
为了做好“双11”促销活动,某电商打算将进行促销活动的礼品重新包装,设计方案如下:将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′,再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示),设AE=BE′=x(cm).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<1 | B. | m>-1 | C. | -1<m<1 | D. | m>1或m<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (${\sqrt{3}$,0) | B. | (${\root{3}{4}$,2] | C. | [${\root{3}{4}$,2) | D. | [${\root{3}{4}$,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com