
分析 (1)利用向量的数量积运算,二倍角余弦公式及变形、两角和的余弦函数公式化简解析式即可;
(2)由余弦函数的增区间和整体思想求出f(x)的增区间.
解答 解:(1)由题意得,向量$\overrightarrow{a}$=(2cos x,sin x),$\overrightarrow{b}$=(cos x,-2cos x),
∴f(x)=$\overrightarrow{a}•\overrightarrow{b}$=2cos2x-2sinxcosx
=1+cos2x-sin2x=$\sqrt{2}cos(2x+\frac{π}{4})+1$,
则f(x)=$\sqrt{2}cos(2x+\frac{π}{4})+1$;
(2)由$-π+2kπ≤2x+\frac{π}{4}≤2kπ(k∈Z)$得,
$-\frac{5π}{8}+kπ≤x≤-\frac{π}{8}+kπ(k∈Z)$,
∴f(x)的单调增区间是$[-\frac{5π}{8}+kπ,-\frac{π}{8}+kπ](k∈Z)$.
点评 本题考查了向量的数量积运算,二倍角余弦公式及变形,两角和的余弦公式,以及余弦函数的单调性,考查整体思想,化简、变形能力.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
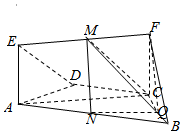 已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.
已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 6.5 | C. | 13 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 阅读过莫言的 作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
| 男生 | 3 | 6 | 11 | 18 | 12 |
| 女生 | 4 | 8 | 13 | 15 | 10 |
| 非常了解 | 一般了解 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com