
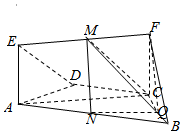
 已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.
已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.分析 (I)取BC的中点Q,连接NQ,FQ,利用三角形中位线定理与平行四边形的判定可得四边形MNQF是平行四边形,因此MN∥FQ,再利用线面平行的判定定理即可证明.
(II)由AB∥CD,AD=DC=CB=1,∠ABC=60°,可得∠ACB=90°,AC=$\sqrt{3}$,AB=2.进而得到FC⊥BC,AC⊥BC,BC⊥平面ACFE.设点A到平面MCB的距离为h,则VA-MCB=$\frac{1}{3}{S}_{△MCB}$•h.四边形ACFE为矩形,又VA-MCB=VB-ACM=$\frac{1}{3}×BC×{S}_{△ACM}$,即可得出.
解答 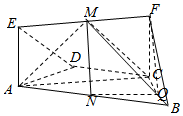 (I)证明:取BC的中点Q,连接NQ,FQ,则NQ=$\frac{1}{2}$AC,NQ∥AC,
(I)证明:取BC的中点Q,连接NQ,FQ,则NQ=$\frac{1}{2}$AC,NQ∥AC,
又MF=$\frac{1}{2}$AC,MF∥AC,
∴MF=NQ,MF∥NQ,则四边形MNQF是平行四边形,
∴MN∥FQ,FQ?平面FCB,MN?平面FCB,
∴MN∥平面FCB.
(II)解:∵AB∥CD,AD=DC=CB=1,∠ABC=60°,可得∠ACB=90°,AC=$\sqrt{3}$,AB=2.
又FC=1,FB=$\sqrt{2}$,BC=1,∴FC⊥BC,又∠ACB=90°,即AC⊥BC.∴BC⊥平面ACFE.
设点A到平面MCB的距离为h,则VA-MCB=$\frac{1}{3}{S}_{△MCB}$•h.
四边形ACFE为矩形,又VA-MCB=VB-ACM=$\frac{1}{3}×BC×{S}_{△ACM}$=$\frac{1}{3}×1×\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{6}$,
S△MCB=$\frac{1}{2}×1×$$\sqrt{1+(\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{7}}{4}$,
∴h=$\frac{\frac{\sqrt{3}}{6}}{\frac{1}{3}×\frac{\sqrt{7}}{4}}$=$\frac{2\sqrt{21}}{7}$,则点A到平面MCB的距离为$\frac{2\sqrt{21}}{7}$.
点评 本题考查了空间位置关系、线面平行的判定定理、三角形中位线定理、平行四边形的判定与性质定理、直角三角形的判定与性质、三棱锥的体积计算公式、“等体积法”,考查了推理能力与计算能力,属于难题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
| P(χ2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | V1=V2 | B. | V1<V2 | C. | V1>V2 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个摩天轮的半径为18m,12分钟旋转一周,它的最低点P0离地面2m,
如图,一个摩天轮的半径为18m,12分钟旋转一周,它的最低点P0离地面2m,| A. | $y=-18cos\frac{π}{12}(x+1)+20$ | B. | $y=-18cos\frac{π}{12}(x-1)+20$ | ||
| C. | $y=-18cos\frac{π}{6}(x+\frac{1}{2})+20$ | D. | $y=-18cos\frac{π}{6}(x-\frac{1}{2})+20$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
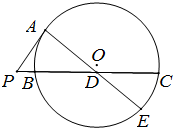 如图,P为⊙O外一点,PA是⊙O的切线,A为切点,割线PBC与⊙O相交于B,C两点,且PC=3PA,D为线段BC的中点,AD的延长线交⊙O于点E.若PB=1,则PA的长为3;AD•DE的值是16.
如图,P为⊙O外一点,PA是⊙O的切线,A为切点,割线PBC与⊙O相交于B,C两点,且PC=3PA,D为线段BC的中点,AD的延长线交⊙O于点E.若PB=1,则PA的长为3;AD•DE的值是16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com