
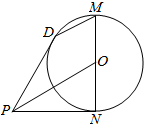
 如图所示,MN为⊙O的直径,PD、PN是切线,切点分别为D和N.
如图所示,MN为⊙O的直径,PD、PN是切线,切点分别为D和N.分析 (1)连结DN、OD,利用PD、PN是切线,所以DN⊥OP,MN为⊙O的直径,所以DM⊥DN,可得∠DOP=∠MDO,即可证明MD∥OP;
(2)证明Rt△NMD~Rt△POD,可得$\frac{MD}{OD}=\frac{NM}{PO}$,即可求MD•OP的值.
解答 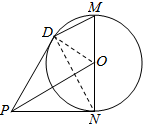 (1)证明:如图,连结DN、OD,
(1)证明:如图,连结DN、OD,
因为PD、PN是切线,所以DN⊥OP,
因此∠DOP+∠ODN=90°,
又因为MN为⊙O的直径,所以DM⊥DN,
因此∠MDO+∠ODN=90°,
于是∠DOP=∠MDO,故MD∥OP.
(2)解:由于∠NMD=∠POD,∴Rt△NMD~Rt△POD,
于是$\frac{MD}{OD}=\frac{NM}{PO}$,因此MD•OP=NM•OD=4×2=8.
点评 本题考查圆的切线的性质,考查直径所对的角为圆周角,考查三角形相似的判定与性质,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 假设三角形的3个内角都大于60° | |
| B. | 假设三角形的3个内角都不大于60° | |
| C. | 假设三角形的3个内角中至多有一个大于60° | |
| D. | 假设三角形的3个内角中至多有两个大于60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
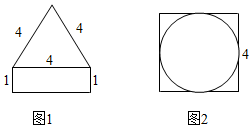 如图1是一个几何体的主视图和左视图(上面是边长为4的正三角形,下面是矩形),图2是它的俯视图(圆内切于边长为4的正方形),则该几何体的体积为16+$\frac{8\sqrt{3}}{3}$π.
如图1是一个几何体的主视图和左视图(上面是边长为4的正三角形,下面是矩形),图2是它的俯视图(圆内切于边长为4的正方形),则该几何体的体积为16+$\frac{8\sqrt{3}}{3}$π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0)∪(0,4] | B. | [-4,0)∪(0,2] | C. | [-4,2] | D. | [-2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}+1$ | B. | $\frac{{2\sqrt{2}}}{3}+1$ | C. | $\sqrt{3}+1$ | D. | $\frac{{3\sqrt{3}}}{4}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
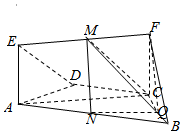 已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.
已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com