
分析 求出f(x)的导数,问题转化为a≥$\frac{1-{4x}^{4}}{{3x}^{3}}$在[3,5]上恒成立,令g(x)=$\frac{1-{4x}^{4}}{{3x}^{3}}$,x∈[3,5],根据函数的单调性求出g(x)的最大值,从而求出a的范围即可.
解答 解:f(x)=x4-lnx+ax3在的定义域是(0,+∞),
f′(x)=4x3-$\frac{1}{x}$+3ax2=$\frac{{4x}^{4}+3{ax}^{3}-1}{x}$,
若f(x)在[3,5]上是增函数,
则a≥$\frac{1-{4x}^{4}}{{3x}^{3}}$在[3,5]上恒成立,
令g(x)=$\frac{1-{4x}^{4}}{{3x}^{3}}$,x∈[3,5],
g′(x)=-$\frac{{4x}^{4}+3}{{3x}^{4}}$<0,
g(x)在[3,5]递减,
g(x)max=g(3)=-$\frac{323}{81}$,
故a≥-$\frac{323}{81}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-2,0)∪(0,4] | B. | [-4,0)∪(0,2] | C. | [-4,2] | D. | [-2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
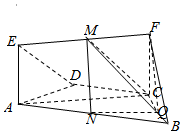 已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.
已知几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE是矩形,FB=$\sqrt{2}$,M,N分别为EF,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
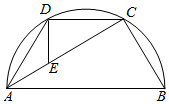 如图,C,D是以AB为直径的半圆上两点,且$\widehat{AD}$=$\widehat{CD}$.
如图,C,D是以AB为直径的半圆上两点,且$\widehat{AD}$=$\widehat{CD}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,∠APC的平分线分别交AB、AC于点D、E,AC=AP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 阅读过莫言的 作品数(篇) | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
| 男生 | 3 | 6 | 11 | 18 | 12 |
| 女生 | 4 | 8 | 13 | 15 | 10 |
| 非常了解 | 一般了解 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com