练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知等比数列{an}，前n项和Sn=3×2n+m，则其公比是（　　）
    A．1B．2C．3D．4

    分析 利用递推关系、等比数列的通项公式及其定义即可得出．

    解答 解：等比数列{an}，前n项和Sn=3×2n+m，
    ∴n≥2时，an=Sn-Sn-1=3×2n+m-（3×2n-1+m）=3×2n-1，
    ∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{3×{2}^{n}}{3×{2}^{n-1}}$=2，
    故选：B．

    点评 本题考查了等比数列的通项公式及其求和公式、递推关系、等比数列的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．如图所示，△ABC是⊙O的内接三角形，且AB=AC，AP∥BC，弦CE的延长线交AP于点D，求证：AD2=DE•DC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

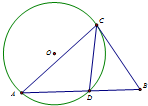    2．如图，弦CD平分∠ACB，BC切⊙O于点C，延长弦AD交BC于点B，若⊙O的半径长为$\frac{5}{2}$，CD=3，则AC=$\frac{24}{5}$，BD=$\frac{25}{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．正态总体N（1，9）在区间（2，3）和（-1，0）上取值的概率分别为m，n，则m=n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知随机变量X服从正态分布X～N（2，σ2），P（X＜4）=0.84，则P（X≤0）的值为0.16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知向量$\overrightarrow{a}$=（2cos x，sin x），$\overrightarrow{b}$=（cos x，-2cos x）．设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$
    （1）求f（x）的解析式
    （2）求f（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知圆C：（x+2）2+y2=4，相互垂直的两条直线l1，l2都过点A（a，0），
    （1）当a=2时，若圆心为M（1，m）（m＞0）的圆和圆C外切且与直线l1，l2都相切，求圆M的方程；
    （2）当a=-1时，记l1，l2被圆C所截得的弦长分别为d1，d2，求：
    ①d12+d22的值；
    ②d1+d2的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

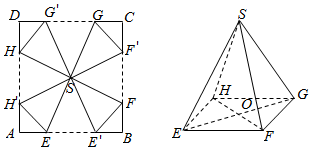    20．为了做好“双11”促销活动，某电商打算将进行促销活动的礼品重新包装，设计方案如下：将一块边长为20cm的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′，△SFF′，△SGG′，△SHH′，再将剩下的阴影部分折成一个四棱锥形状的礼品袋S-EFGH，其中A，B，C，D重合于点O，E与E′重合，F与F′重合，G与G′重合，H与H′重合（如图所示），设AE=BE′=x（cm）．
    （1）求证：平面SEG⊥平面SFH；
    （2）若电商要求礼品袋的侧面积不少于128cm2，试求x的取值范围；
    （3）当x=5时，该电商打算将礼品袋S-EFGH全部放入一个球形状的包装盒内密封，求包装盒的内径R的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

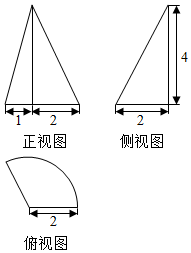
    1．某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的表面积为（　　）
    A．$\frac{4\sqrt{5}π+4π}{3}$B．$\frac{2\sqrt{5}π+4π}{3}$C．$\frac{12+4\sqrt{5}π+4π}{3}$D．$\frac{24+4\sqrt{5}π+4π}{3}$

    查看答案和解析>>

    同步练习册答案