Question

1．某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的表面积为（　　）

• A． $\frac{4\sqrt{5}π+4π}{3}$
• B． $\frac{2\sqrt{5}π+4π}{3}$
• C． $\frac{12+4\sqrt{5}π+4π}{3}$
• D． $\frac{24+4\sqrt{5}π+4π}{3}$

Answer 1

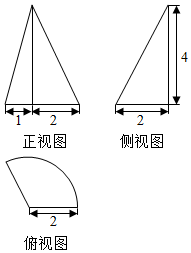
分析 根据三视图判断几何体是圆锥的一部分，再根据俯视图与左视图的数据可求得底面扇形的圆心角为120°，又由侧视图知几何体的高为4，底面圆的半径为2，把数据代入圆锥的表面积公式计算．

解答 解：由三视图知，该几何体是圆锥的一部分，底面为扇形，圆心角为120°，半径为2，锥体的高为4．
其表面积为：$\frac{1}{2}×2×4×2$+$\frac{1}{2}×\frac{1}{3}×2π×2×2\sqrt{5}$+$\frac{1}{3}×π×{2}^{2}$=$\frac{24+4\sqrt{5}π+4π}{3}$．
故选D．

点评 本题考查的知识点是由三视图求表面积，其中根据已知的三视图分析出几何体的形状是解答的关键．