
分析 利用等差数的通项公式可得bn,再利用“累加求和”方法与等差数列的求和公式即可得出an.
解答 解:设等差数列{bn}的公差为d,∵b3=-2,b10=12.∴b1+2d=-2,b1+9d=12,解得b1=-6,d=2.∴bn=-6+2(n-1)=2n-8.
∵bn=an+1-an(n∈N*),
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=(2n-10)+(2n-12)+…+(-6)+3
=$\frac{(n-1)(-6+2n-10)}{2}$+3
=n2-9n+11.
当n=10时,a10=102-9×10+11=21.
故答案为:21.
点评 本题考查了等差数列的通项公式及其求和公式、“累加求和”方法,考查了推理能力与计算能力,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<1 | B. | m>-1 | C. | -1<m<1 | D. | m>1或m<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
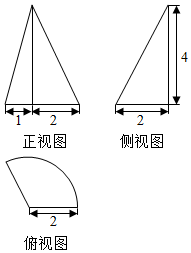
| A. | $\frac{4\sqrt{5}π+4π}{3}$ | B. | $\frac{2\sqrt{5}π+4π}{3}$ | C. | $\frac{12+4\sqrt{5}π+4π}{3}$ | D. | $\frac{24+4\sqrt{5}π+4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1,3} | C. | {1,5} | D. | {2,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (${\sqrt{3}$,0) | B. | (${\root{3}{4}$,2] | C. | [${\root{3}{4}$,2) | D. | [${\root{3}{4}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b>0 | B. | a-b<0 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ab<b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com