
【题目】如图,已知动直线l过点 ![]() ,且与圆O:x2+y2=1交于A、B两点.
,且与圆O:x2+y2=1交于A、B两点. 
(1)若直线l的斜率为 ![]() ,求△OAB的面积;
,求△OAB的面积;
(2)若直线l的斜率为0,点C是圆O上任意一点,求CA2+CB2的取值范围;
(3)是否存在一个定点Q(不同于点P),对于任意不与y轴重合的直线l,都有PQ平分∠AQB,若存在,求出定点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:因为直线l的斜率为 ![]() ,所以直线l
,所以直线l ![]() ,
,
则点O到直线l的距离 ![]() ,
,
所以弦AB的长度 ![]() ,
,
所以 ![]()
(2)解:因为直线l的斜率为0,所以可知 ![]() 、
、 ![]()
设点C(x,y),则x2+y2=1,
又 ![]() ,
,
所以CA2+CB2=4﹣2y,又y∈[﹣1,1],
所以CA2+CB2的取值范围是[2,6]
(3)解:法一:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1,y1)、B(x2,y2),
因直线l不与y轴重合,设直线l ![]() ,
,
代入圆O得 ![]() ,
,
所以 ![]() (*)
(*)
若PQ平分∠AQB,则根据角平分线的定义,AQ与BQ的斜率互为相反数
有 ![]() ,又
,又 ![]() ,
, ![]() ,
,
化简可得 ![]() ,
,
代入(*)式得 ![]() ,因为直线l任意,故
,因为直线l任意,故 ![]() ,
,
即t=2,即Q(0,2)
解法二:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1,y1)、B(x2,y2),
因直线l不与y轴重合,设直线l ![]() ,
,
代入圆O得 ![]() ,
,
所以 ![]() (*)
(*)
若PQ平分∠AQB,则根据角平分线的几何意义,点A到y轴的距离d1,点B到y轴的距离d2满足 ![]() ,即
,即 ![]() ,
,
化简可得 ![]() ,
,
代入(*)式得 ![]() ,因为直线l任意,故
,因为直线l任意,故 ![]() ,
,
即t=2,即Q(0,2)
【解析】(1)因为直线l的斜率为 ![]() ,所以直线l
,所以直线l ![]() ,利用弦长、半径、弦心距的关系,求得弦长及△OAB的高,即可求出面积.(2)因为直线l的斜率为0,所以可知
,利用弦长、半径、弦心距的关系,求得弦长及△OAB的高,即可求出面积.(2)因为直线l的斜率为0,所以可知 ![]() 、
、 ![]() ,设点C(x,y),则x2+y2=1,又
,设点C(x,y),则x2+y2=1,又 ![]() =4﹣2y,又y∈[﹣1,1],即可得CA2+CB2的取值范围.(3)法一:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1 , y1)、B(x2 , y2),因直线l不与y轴重合,设直线l
=4﹣2y,又y∈[﹣1,1],即可得CA2+CB2的取值范围.(3)法一:若存在,则根据对称性可知,定点Q在y轴上,设Q(0,t)、又设A(x1 , y1)、B(x2 , y2),因直线l不与y轴重合,设直线l ![]() ,代入圆O得
,代入圆O得 ![]() ,所以
,所以 ![]() (*)由AQ与BQ的斜率互为相反数,可得
(*)由AQ与BQ的斜率互为相反数,可得 ![]() ,即求得t;解法二:若PQ平分∠AQB,则根据角平分线的几何意义,点A到y轴的距离d1 , 点B到y轴的距离d2满足
,即求得t;解法二:若PQ平分∠AQB,则根据角平分线的几何意义,点A到y轴的距离d1 , 点B到y轴的距离d2满足 ![]() ,即
,即 ![]() ,化简可得
,化简可得 ![]() ,同时求得t.
,同时求得t.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
则x,y的值分别为( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 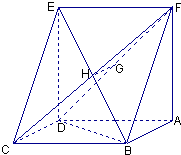
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱锥F﹣ABCD的体积.
,求四棱锥F﹣ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)当a=1时,求f(x)在[1,4]上的最大值和最小值.
(2)若f (x)在( ![]() ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln x+![]() (a>0).
(a>0).
(1)求函数f(x)的极值;
(2)若对任意的x>0,恒有ax(2-ln x)≤1,求实数a的取值范围;
(3)是否存在实数a,使得函数f(x)在[1,e]上的最小值为0?若存在,试求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学校食堂的服务情况,随机调查了50名就餐的教师和学生.根据这50名师生对餐厅服务质量进行评分,绘制出了频率分布直方图(如图所示),其中样本数据分组为[40,50),[50,60),…,[90,100]. 
(1)求频率分布直方图中a的值;
(2)从评分在[40,60)的师生中,随机抽取2人,求此人中恰好有1人评分在[40,50)上的概率;
(3)学校规定:师生对食堂服务质量的评分不得低于75分,否则将进行内部整顿,试用组中数据估计该校师生对食堂服务质量评分的平均分,并据此回答食堂是否需要进行内部整顿.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x﹣y|=2”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com