
【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | ≥4 |
保费(元) |
|
|
|
|
|
随机调查了该险种的![]() 名续保人在一年内的出险情况,得到下表:
名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 | ≥4 |
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
|
|
将所抽样本的频率视为概率.
(1)求本年度续保人保费的平均值的估计值;
(2)按保险合同规定,若续保人在本年度内出险![]() 次,则可获得赔付
次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(3)续保人原定约了保险公司的销售人员在上午![]() 之间上门签合同,因为续保人临时有事,外出的时间在上午
之间上门签合同,因为续保人临时有事,外出的时间在上午![]() 之间,请问续保人在离开前见到销售人员的概率是多少?
之间,请问续保人在离开前见到销售人员的概率是多少?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)得出保费![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 对应的概率,即可得出本年度续保人保费的平均值的估计值;
对应的概率,即可得出本年度续保人保费的平均值的估计值;
(2)先计算出每个赔偿金额对应的概率,然后按照平均值的计算公式得出本年度续保人所获赔付金额的平均值的估计值;
(3)由几何概型概率公式计算即可.
解:(1)由题意可得
保费(元) |
|
|
|
|
|
概率 | 0.7 | 0.2 | 0.06 | 0.03 | 0.01 |
本年度续保人保费的平均值的估计值为
![]()
(2)由题意可得
赔偿金额(元) | 0 |
|
|
|
|
概率 | 0.7 | 0.2 | 0.06 | 0.03 | 0.01 |
本年度续保人所获赔付金额的平均值的估计值
![]()
(3)设保险公司销售人员到达的时间为![]() ,续保人离开的时间为
,续保人离开的时间为![]() ,
,![]() 看成平面上的点,全部结果所构成的区域为
看成平面上的点,全部结果所构成的区域为![]()
则区域![]() 的面积
的面积![]()
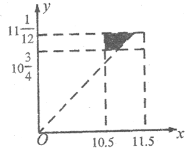
事件![]() 表示续保人在离开前见到销售人员,所构成的区域为
表示续保人在离开前见到销售人员,所构成的区域为![]()
即图中的阴影部分,其面积![]()
所以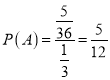 ,即续保人在离开前见到销售人员的概率是
,即续保人在离开前见到销售人员的概率是![]()


科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢宾斯基三角形是一种分形,由波兰数学家谢宾斯基在1915年提出,先作一个正三角形.挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色代表挖去的面积,那么黑三角形为剩下的面积(我们称黑三角形为谢宾斯基三角形).向图中第5个大正三角形中随机撒512粒大小均匀的细小颗粒物,则落在白色区域的细小颗粒物的数量约是( )

A.256B.350C.162D.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市工会组织了一次工人综合技能比赛,一共有![]() 名工人参加,他们的成绩都分布在
名工人参加,他们的成绩都分布在![]() 内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在
内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在![]() 分及
分及![]() 分以上的为优秀.
分以上的为优秀.

(1)求图中![]() 的值;
的值;
(2)估计这次比赛成绩的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(3)某工厂车间有![]() 名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于
名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为迎接一项重要的体育赛事,要完成![]() ,
,![]() 两座场馆的地基建造工程.某工程队需要把600名工人分成两组,一组完成
两座场馆的地基建造工程.某工程队需要把600名工人分成两组,一组完成![]() 场馆的甲级标准地基2000
场馆的甲级标准地基2000![]() ,同时另一组完成
,同时另一组完成![]() 场馆的乙级标准地基3000
场馆的乙级标准地基3000![]() ;据测算,完成甲级标准地基每平方米的工程量为50人
;据测算,完成甲级标准地基每平方米的工程量为50人![]() 天,完成乙级标准地基每平方米的工程量为30人
天,完成乙级标准地基每平方米的工程量为30人![]() 天.
天.
(1)若工程队分配![]() 名工人去
名工人去![]() 场馆,求
场馆,求![]() 场馆地基和
场馆地基和![]() 场馆地基建造时间
场馆地基建造时间![]() 和
和![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)![]() 、
、![]() 两个场馆同时开工,该工程队如何分配两个场馆的工人数量,可以使得工期最短.
两个场馆同时开工,该工程队如何分配两个场馆的工人数量,可以使得工期最短.
(参考数据:![]() ,
,![]() ,
,![]() .备注:若地基面积为
.备注:若地基面积为![]() 平方米,每平方米的工程量为
平方米,每平方米的工程量为![]() 人/天,工人数
人/天,工人数![]() 人,则工期为
人,则工期为![]() 天.)
天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
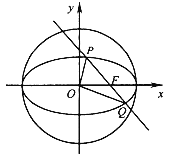
(1)求椭圆C的标准方程;
(2)设过F的直线l与椭圆C相交于P,Q两点.已知l被圆O:x2+y2=a2截得的弦长为![]() ,求△OPQ的面积.
,求△OPQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程,并说明它是何种曲线;
的直角坐标方程,并说明它是何种曲线;
(2)设点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,证明:直线
两点,证明:直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com