解:(Ⅰ)由a
1=1及b
n=n+1,令n=1,得到a
2=a
1+b
1=1+2=3,
令n=2,得到a
3=a
2+b
2=3+3=6,
令n=4,得到a
4=a
3+b
3=6+4=10;
(Ⅱ)(ⅰ)因为b
n+1b
n-1=b
n(n≥2),
所以,对任意的n∈N
*有
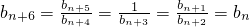
,
即数列{b
n}各项的值重复出现,周期为6.(5分)
又数列{b
n}的前6项分别为
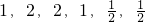
,且这六个数的和为7.
设数列{b
n}的前n项和为S
n,
则当n=2k(k∈N
*)时,S
3n=S
6k=k(b
1+b
2+b
3+b
4+b
5+b
6)=7k,
当n=2k+1(k∈N
*)时,S
3n=S
6k+3=k(b
1+b
2+b
3+b
4+b
5+b
6)+b
6k+1+b
6k+2+b
6k+3=7k+b
1+b
2+b
3=7k+5,(7分)
所以,当n为偶数时,
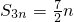
;当n为奇数时,
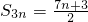
.(8分)
(ⅱ)证明:由(ⅰ)知:对任意的n∈N
*有b
n+6=b
n,
又数列{b
n}的前6项分别为

,且这六个数的和为
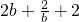
.
设c
n=a
6n+i(n≥0),(其中i为常数且i∈{1,2,3,4,5,6}),
所以c
n+1-c
n=a
6n+6+i-a
6n+i=b
6n+i+1+b
6n+i+2+b
6n+i+3+b
6n+i+4+b
6n+i+5+b
6n+i+6=
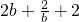
.
所以,数列{a
6n+i}均为以
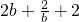
为公差的等差数列.(10分)
因为b>0时,
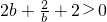
,b<0时,
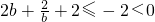
,(12分)
所以{a
6n+i}为公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次.
所以数列{a
n}中任意一项的值最多在此数列中出现6次,即任意一项的值不会在此数列中重复出现无数次.(14分)
分析:(Ⅰ)根据数列{a
n}的首项为1,把n=1代入b
n=a
n+1-a
n及b
n=n+1中,得到数列{a
n}第2项的值,由求出的第2项的值和n=2代入求出的b
2,即可求出数列{a
n}第3项的值,由求出的第3项的值和n=3代入求出的b
3,即可求出数列{a
n}第4项a
4的值;
(Ⅱ)(ⅰ)根据已知的条件b
n+1b
n-1=b
n,当n大于等于2时,把n换为n+6,代入已知的等式后,化简得到b
n+6=b
n,得到数列{b
n}各项的值重复出现,周期为6,又b
1=a=1,b
2=b=2,根据b
n+1b
n-1=b
n,依次得到b
3,b
4,b
5,b
6的值,且求出六个数的和,设数列{b
n}的前n项和为S
n,然后分n为偶数即n=2k和n为奇数即n=2k+1两种情况考虑,当n=2k时,S
3n等于S
6k,根据数列{b
n}各项的值重复出现,周期为6,得到S
3n等于S
6k等于前6项之和的k倍,即可求出S
3n的值,当n=2k+1时,S
3n等于S
6k+3等于前6项之和的k倍加上第6k+1,6k+2,6k+3三项,又根据数列{b
n}各项的值重复出现,周期为6,得到S
3n等于S
6k+3等于7k加上第1、2及3项的和,进而得到S
3n的值;
(ⅱ)由(i)得到数列{b
n}各项的值重复出现,周期为6,b
1=a=1,再根据b
n+1b
n-1=b
n,第2项等于b,即可表示出第3项到第6项的值,且表示出六项的和,设c
n=a
6n+i,所以c
n+1-c
n,根据数列的周期性得到之差等于前6项的和,数列{a
6n+i}均为等差数列,公差为前6项的和,当b大于0时,得到公差大于0,当b小于0时得到公差小于0,所以{a
6n+i}为公差不为零的等差数列,其中任何一项的值最多在该数列中出现一次.即数列{a
n}中任意一项的值最多在此数列中出现6次不会出现无数次,得证.
点评:此题考查学生会利用数列的递推式得到数列的特征及周期性,根据数列的递推式及周期性求出数列的和,是一道中档题.

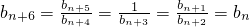 ,
,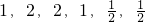 ,且这六个数的和为7.
,且这六个数的和为7.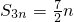 ;当n为奇数时,
;当n为奇数时,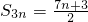 .(8分)
.(8分) ,且这六个数的和为
,且这六个数的和为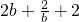 .
.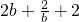 .
.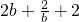 为公差的等差数列.(10分)
为公差的等差数列.(10分)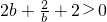 ,b<0时,
,b<0时,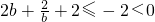 ,(12分)
,(12分)

 名校课堂系列答案
名校课堂系列答案