练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，角A、B、C的对边分别是．已知
    （1）求角C的大小；
    （2）若，求△ABC外接圆半径．

    （1）（2）．

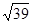    解析试题分析：（1）由三角函数给值求角知识可知：要求角的大小，首先必须明确角的范围，再就是求出角的某一三角函数值；因此既然是求角Ｃ，而已知等式中只含有角Ｃ，所以只须将cosC移到等式的右侧，逆用余弦倍角公式，左边用正弦的倍角公式化成再注意到，从而可得，然后两边一平方就可求得sinC=,但不能就此得到角C为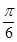，还必须注意到，所以（2）由正弦定理可知：△ABC外接圆半径R满足，由(1)知角C的大小,所以只需求出边c即可；注意观察已知等式知可分别按边a,b配方得到从而得到再用余弦定理就可求出边c，进而就可求得三角形的外接圆半径．
    试题解析：（1）∵即
    由，∴,即
    ∵，得即，所以
    （2）由得得
    ∴∴．
    考点：１．三角公式；２．正弦定理和余弦定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    地面上有两座塔AB、CD，相距120米，一人分别在两塔底部测得一塔顶仰角为另一塔顶仰角的2倍，在两塔底连线的中点O测得两塔顶的仰角互为余角，求两座塔的高度。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，角A，B，C所对的边分别为,设S为△ABC的面积，且。
    （Ⅰ）求角A的大小；
    （Ⅱ）若，求△ABC周长的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在中，内角的对边分别为，满足．
    （1）求角的度数；
    （2）若求周长的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，设A、B、C的对边分别为a、b、c，向量,,若
    （1）求角A的大小；
    （2）若的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，A、B、C所对的边分别是a、b、c，bcos B是acos C，ccos A的等差中项．
    （1）求B的大小；
    （2）若，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在△ABC中，内角A，B，C所对的边分别为a，b，c，已知sin B(tan A＋tan C)＝tan Atan C.
    (1)求证：a，b，c成等比数列；
    (2)若a＝1，c＝2，求△ABC的面积S.

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    在中，BD为的平分线，已知，
    则_____________；               　　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    设上的奇函数，且在区间（0，）上单调递增，若
    ，三角形的内角A满足，则A的取值范围是        

    查看答案和解析>>

    同步练习册答案