
(本小题满分14分)
已知函数 (
(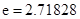 …是自然对数的底数)的最小值为
…是自然对数的底数)的最小值为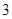 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)已知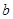
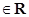 且
且 ,试解关于
,试解关于 的不等式
的不等式 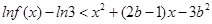 ;
;
(Ⅲ)已知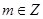 且
且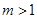 .若存在实数
.若存在实数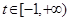 ,使得对任意的
,使得对任意的 ,都有
,都有 ,试求
,试求 的最大值.
的最大值.
(1)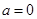 (2)构造函数运用导数求解最值得到不等式的证明。
(2)构造函数运用导数求解最值得到不等式的证明。
(3) 满足条件的最大整数 的值为3.
的值为3.
解析试题分析:解:(Ⅰ)因为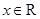 ,所以
,所以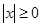 ,故
,故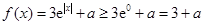 ,
,
因为函数 的最小值为
的最小值为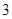 ,所以
,所以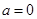 . ……………… 3分
. ……………… 3分
(Ⅱ)由(Ⅰ)得,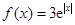 .
.
当 时,
时,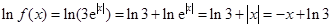 ,……… 5分
,……… 5分
故不等式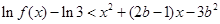 可化为:
可化为: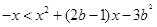 ,
,
即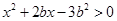 , ……………… 6分
, ……………… 6分
得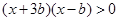 ,
,
所以,当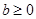 时,不等式的解为
时,不等式的解为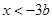 ;
;
当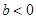 时,不等式的解为
时,不等式的解为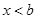 . …………… 8分
. …………… 8分
(Ⅲ)∵当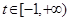 且
且 时,
时,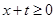 ,
,
∴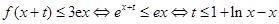 .
.
∴原命题等价转化为:存在实数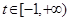 ,使得不等式
,使得不等式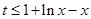 对任意
对任意 恒成立. …………… 10分
恒成立. …………… 10分
令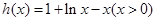 .
.
∵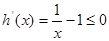 ,∴函数
,∴函数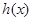 在
在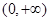 为减函数. …………… 11分
为减函数. …………… 11分
又∵ ,∴
,∴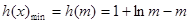 . …………… 12分
. …………… 12分
∴要使得对 ,
,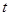 值恒存在,只须
值恒存在,只须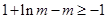 .………… 13分
.………… 13分
∵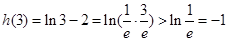 ,
,
且函数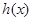 在
在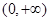 为减函数,
为减函数,
∴满足条件的最大整数 的值为3.…… 14分
的值为3.…… 14分
考点:导数,函数。
点评:本小题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等,属于中档题。


科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 在区间
在区间 上是减函数.
上是减函数.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若 在
在 上恒成立,求实数
上恒成立,求实数 的最大值;
的最大值;
(Ⅲ)若关于 的方程
的方程 有且只有一个实数根,求
有且只有一个实数根,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数
(1) 当a= -1时,求函数的最大值和最小值;
(2) 求实数a的取值范围,使y=f(x)在区间 上是单调函数
上是单调函数
(3) 求函数f(x)的最小值g(a),并求g(a)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数
(Ⅰ)若函数 处取得极值,求实数a的值;
处取得极值,求实数a的值;
(Ⅱ)在(I)条件下,若直线 与函数
与函数 的图象相切,求实数k的值;
的图象相切,求实数k的值;
(Ⅲ)记 ,求满足条件的实数a的集合.
,求满足条件的实数a的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: <ln(x+1)<x;
<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com