
设函数f(x)=ax-(a+1)ln(x+1),其中a>0.
(1)求f(x)的单调区间;
(2)当x>0时,证明不等式: <ln(x+1)<x;
<ln(x+1)<x;
(3)设f(x)的最小值为g(a),证明不等式:-1<ag(a)<0
(1) f(x)在(-1,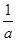 )为减,在(
)为减,在(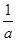 ,+
,+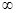 )为增
)为增
(2)将所证明的不等式利用构造函数,借助于导数的思想求解最值,来证明不等式恒大于等于零或者恒小于等于零即可。
(3)在上一问的基础上,进一步分析得到a的表达式,利用构造函数来求证。
解析试题分析:解:(1)f’(x)=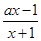 (x>-1,a>0)
(x>-1,a>0)
令f’(x)=0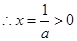
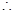 f(x)在(-1,
f(x)在(-1,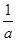 )为减,在(
)为减,在(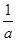 ,+
,+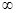 )为增 f (x)min=f(
)为增 f (x)min=f(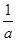 )=1-(a+1)ln(
)=1-(a+1)ln(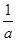 +1)
+1)
(2)设F(x)=ln(x+1)-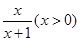
F’(x)=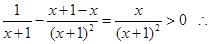 F(x)在(0,+
F(x)在(0,+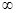 )为增函数
)为增函数
F(x)>F(0)="0" 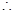 F(x)>0即
F(x)>0即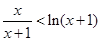
G(x)=x-ln(x+1)(x>0)
G’(x)=1-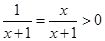
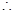 G(x)在(0,+
G(x)在(0,+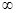 )为增函数
)为增函数
G(x)>G(0)="0" 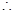 G(x)>0即ln(x+1)<x
G(x)>0即ln(x+1)<x
经上可知
(3)由(1)知:
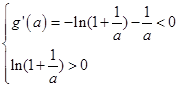
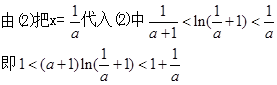
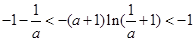
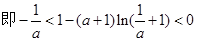
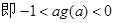
考点:本试题主要是考查了导数在研究函数中的运用。
点评:导数在函数中的应用,频率最多的试题就是考查函数的单调性,以及证明不等式。那么对于后者的求解,关键是构造函数,借助于函数的最值来得到证明。


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 (
(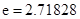 …是自然对数的底数)的最小值为
…是自然对数的底数)的最小值为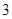 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)已知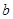
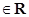 且
且 ,试解关于
,试解关于 的不等式
的不等式 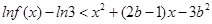 ;
;
(Ⅲ)已知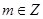 且
且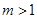 .若存在实数
.若存在实数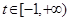 ,使得对任意的
,使得对任意的 ,都有
,都有 ,试求
,试求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, ,(
,( 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)函数 在区间
在区间 上恒为正数,求
上恒为正数,求 的最小值;
的最小值;
(Ⅲ)若对任意给定的 ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
一片森林原来面积为 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的 .
.
(Ⅰ)求每年砍伐面积的百分比;
(Ⅱ)到今年为止,该森林已砍伐了多少年?
(Ⅲ)今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为 的不动点,已知函数
的不动点,已知函数 (a≠0).
(a≠0).
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数b,函数 恒有两个相异的不动点,求a的取值范围;
恒有两个相异的不动点,求a的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com