
| A. | $({0,\frac{1}{8}}]$ | B. | $({0,\frac{5}{8}}]$ | C. | $({0,\frac{1}{8}}]∪[{\frac{5}{8},1}]$ | D. | $({0,\frac{1}{8}}]∪[{\frac{1}{4},\frac{5}{8}}]$ |
分析 利用两角和与差的三角函数化简函数的解析式,利用函数的零点以及函数的周期,列出不等式求解即可.
解答 解:$\overrightarrow a=({sin\frac{ω}{2}x,sinωx}),\overrightarrow b=({sin\frac{ω}{2}x,\frac{1}{2}})$,其中ω>0,
则函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$=sin2($\frac{ω}{2}$x)+$\frac{1}{2}$sinωx-$\frac{1}{2}$=$\frac{1}{2}$-$\frac{1}{2}$cosωx+$\frac{1}{2}$sinωx-$\frac{1}{2}$=$\sqrt{2}$sin(ωx-$\frac{π}{4}$),
可得T=$\frac{2π}{ω}$≥π,0<ω≤2,f(x)在区间(π,2π)内没有零点,结合三角函数可得,
$\left\{\begin{array}{l}{πω-\frac{π}{4}≥0}\\{2πω-\frac{π}{4}≤π}\end{array}\right.$或$\left\{\begin{array}{l}{πω-\frac{π}{4}≥π}\\{2πω-\frac{π}{4}≤2π}\end{array}\right.$,
解得$\frac{1}{4}$≤ω≤$\frac{5}{8}$或0<ω≤$\frac{1}{8}$,
故选:D.
点评 本题考查函数的零点个数的判断,三角函数的化简求值,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
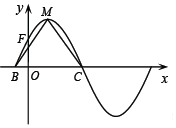 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,M为最高点,该图象与y轴交于点F(0,$\sqrt{2}$),与x轴交于点B,C,且△MBC的面积为π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 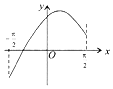 | B. | 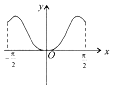 | C. | 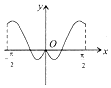 | D. | 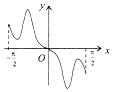 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com