
ЗжЮі гЩЬтвтЃЌЩш$\overrightarrow{c}$=ЃЈxЃЌyЃЉЃЌЕУЕНЃЈ$\overrightarrow{a}-\overrightarrow{c}$ЃЉКЭЃЈ$\overrightarrow{c}-\overrightarrow{b}$ЃЉЕФзјБъЃЌРћгУДЙжБЕФаджЪЕУЕНЙигкxЃЌyЕШЪНЃЌдйЧѓФЃЕФЗЖЮЇЃЎ
НтД№ НтЃКЩш$\overrightarrow{c}$=ЃЈxЃЌyЃЉЃЌ
дђ$\overrightarrow{a}-\overrightarrow{c}$=ЃЈ3-xЃЌ-yЃЉЃЌ$\overrightarrow{c}-\overrightarrow{b}$=ЃЈxЃЌy-2ЃЉЃЌ
вђЮЊЃЈ$\overrightarrow{a}-\overrightarrow{c}$ЃЉЁЭЃЈ$\overrightarrow{c}-\overrightarrow{b}$ЃЉЃЌ
ЫљвдЃЈ$\overrightarrow{a}-\overrightarrow{c}$ЃЉ•ЃЈ$\overrightarrow{c}-\overrightarrow{b}$ЃЉ=0ЃЌМДЃЈ3-xЃЉx-yЃЈy-2ЃЉ=0ЃЌ
ЫљвдЃЈx-$\frac{3}{2}$ЃЉ2+ЃЈy-1ЃЉ2=$\frac{13}{4}$ЃЌ
Ыљвд|$\overrightarrow{c}$|=$\sqrt{{x}^{2}+{y}^{2}}$ЃЌБэЪОдВЩЯЕФЕуЕНдЕуЕФОрРыЃЌ
ЫљвдзюДѓжЕЮЊ$\frac{\sqrt{13}}{2}ЁС2=\sqrt{13}$ЃЌзюаЁжЕЮЊ0ЃЛ
Ыљвд|$\overrightarrow{c}$|ЕФШЁжЕЗЖЮЇЮЊ[0ЃЌ$\sqrt{13}$]ЃЎ
ЕуЦР БОЬтПМВщСЫЯђСПЕФзјБъдЫЫуЁЂЯђСПДЙжБЕФаджЪвдМАРћгУЯђСПЕФФЃЕФМИКЮвтвхЧѓФЃЕФзюжЕЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2017НьНЮїФЯВ§аТПЮБъИпШ§вЛТжИДЯАбЕСЗШ§Ъ§бЇЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
КЏЪ§ ЕФЖЈвхгђЮЊ ЃЎ
ЕФЖЈвхгђЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{1}{2}$ | BЃЎ | $\frac{\sqrt{2}}{2}$ | CЃЎ | $\frac{2}{3}$ | DЃЎ | $\frac{\sqrt{3}}{2}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2017НьАВЛеЛДББЪЎЖўжаИпШ§ЩЯдТПМЖўЪ§бЇЃЈРэЃЉЪдОэЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
вбжЊУќЬт Йигк
Йигк ЕФЗНГЬ
ЕФЗНГЬ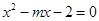 дк
дк гаНтЃЌУќЬт
гаНтЃЌУќЬт дк
дк ЕЅЕїЕндіЃЛШє
ЕЅЕїЕндіЃЛШє ЮЊецУќЬтЃЌ
ЮЊецУќЬтЃЌ ЪЧецУќЬтЃЌЧѓЪЕЪ§
ЪЧецУќЬтЃЌЧѓЪЕЪ§ ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com