
【题目】已知三个集合U,A,B及元素间的关系如图所示,则(CUA)∩B=( ) 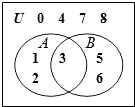
A.{5,6}
B.{3,5,6}
C.{3}
D.{0,4,5,6,7,8}
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若关于x的方程f(f(x))=0有且只有一个实数解,则实数a的取值范围是( )
,若关于x的方程f(f(x))=0有且只有一个实数解,则实数a的取值范围是( )
A.(﹣∞,0)
B.(﹣∞,0]∪(0,1)
C.(﹣∞,0)∪(0,1]
D.(﹣∞,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的图象过点(0,﹣1).
的图象过点(0,﹣1).
(1)求实数a的值;
(2)若f(x)=m+ ![]() (m,n是常数),求实数m,n的值;
(m,n是常数),求实数m,n的值;
(3)用定义法证明:函数f(x)在(3,+∞)上是单调减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,
x | ﹣1 | 0 | 4 |
f(x) | 1 | 2 | 2 |
f(x)的导函数y=f′(x)的图象(该图象关于(2,0)中心对称) 如图所示.
下列关于f(x)的命题:
①函数f(x)的极大值点为 0与4;
②函数f(x)在[0,2]上是减函数;
③函数y=f(x)﹣a零点的个数可能为0、1、2、3、4个;
④如果当时x∈[﹣1,t],f(x)的最大值是2,那么t的最大值为5;.
⑤函数f(x)的图象在a=1是上凸的
其中一定正确命题的序号是 . 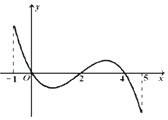
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a是常数,且a>0).对于下列命题:①函数f(x)的最小值是﹣1;②函数f(x)在R上是单调函数;③若f(x)>0在[
(a是常数,且a>0).对于下列命题:①函数f(x)的最小值是﹣1;②函数f(x)在R上是单调函数;③若f(x)>0在[ ![]() ,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2 , 恒有f(
,+∞)上恒成立,则a的取值范围是a>1;④对任意x1<0,x2<0且x1≠x2 , 恒有f( ![]() )>
)> ![]() .其中正确命题的序号是( )
.其中正确命题的序号是( )
A.①②
B.①③
C.③④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,具有线性相关关系,下表为抽样试验的结果:
转速x(转/秒) | 8 | 10 | 12 | 14 | 16 |
每小时生产有缺点的零件数y(件) | 5 | 7 | 8 | 9 | 11 |
参考公式: ![]() ,
, ![]() =
= 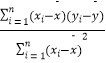 =
= 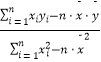 .
.
(1)如果y对x有线性相关关系,求回归方程;
(2)若实际生产中,允许每小时生产的产品中有缺点的零件最多有10个,那么机器的运转速度应控制在设么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2n2+n,n∈N* , 数列{bn}满足an=4log2bn+3,n∈N* .
(1)求an , bn;
(2)求数列{anbn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[ ![]() ]表示不超过
]表示不超过 ![]() 的最大整数.若 S1=[
的最大整数.若 S1=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=3,
]=3,
S2=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=10,
]=10,
S3=[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]+[
]+[ ![]() ]=21,
]=21,
…,
则Sn=( )
A.n(n+2)
B.n(n+3)
C.(n+1)2﹣1
D.n(2n+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com