
分析 化参数方程与普通方程,求出圆的圆心与半径,求出切线的斜率,然后求解切线方程,转化为极坐标方程.
解答 解:因为曲线C的参数方程为$\left\{\begin{array}{l}{x=\sqrt{2}cost}\\{y=\sqrt{2}sint}\end{array}\right.$(t为参数),
所以其普通方程为x2+y2=2,即曲线C为以原点为圆心,$\sqrt{2}$为半径的圆.…(5分)
由于点(1,1)在圆上,且该圆过(1,1)点的半径的斜率为1,
所以切线l的斜率为-1,其普通方程为x+y-2=0,
化为极坐标方程为ρcosθ+ρsinθ=2,即$ρsin(θ+\frac{π}{4})=\sqrt{2}$.…(10分)
点评 本题考查参数方程与普通方程以及极坐标方程的互化,直线与圆的位置关系的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AB=BC,点M,N分别为PC,AC的中点.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AB=BC,点M,N分别为PC,AC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若该大学某女生身高增加1cm,则其体重约增加0.85kg | |
| B. | 回归直线过样本的中心($\overline{x}$,$\overline{y}$) | |
| C. | y与x具有正的线性相关关系 | |
| D. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [2,+∞) | C. | (-∞,1] | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
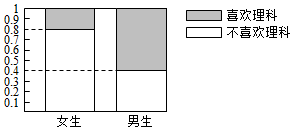
| A. | 性别与是否喜欢理科无关 | B. | 女生中喜欢理科的比为80% | ||
| C. | 男生比女生喜欢理科的可能性大 | D. | 男生中喜欢理科的比例为80% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com