
���� ��1�����ݺ�����ͼ������������������ں��������Ϻ�������ż�Խ�����⼴�ɣ�
��2�����ݺ������������k��ֵ�����ú����뷽��֮��Ĺ�ϵ������⼴�ɣ�
��� 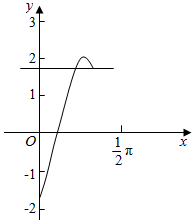 �⣺��1���ߺ���f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}��$��ͼ����y���Ҳ���x���һ������͵�һ����ߵ������ֱ�Ϊ��x0��0���ͣ�x0+$\frac{��}{2}$��2����
�⣺��1���ߺ���f��x��=Asin����x+�գ���A��0���أ�0��|��|��$\frac{��}{2}��$��ͼ����y���Ҳ���x���һ������͵�һ����ߵ������ֱ�Ϊ��x0��0���ͣ�x0+$\frac{��}{2}$��2����
��A=2��$\frac{T}{4}$=$\frac{��}{2}$����T=2��=$\frac{2��}{��}$��
���=1��
��f��x��=2sin��x+�գ���
��������f��x����ͼ������ƽ��$\frac{��}{3}$����λ�����ú���ͼ�����ԭ��Գƣ�
��y=2sin��x+$\frac{��}{3}$+�գ����溯����
��|��|��$\frac{��}{2}$��
��-$\frac{��}{2}$���գ�$\frac{��}{2}$��
��-$\frac{��}{6}$����+$\frac{��}{3}$��$\frac{5��}{6}$��
���+$\frac{��}{3}$=0��
����=-$\frac{��}{3}$��
����f��x���Ľ���ʽf��x��=2sin��x-$\frac{��}{3}$����
��2������y=f��kx��+1=2sin��kx-$\frac{��}{3}$��+1��
�ߺ���y=f��kx��+1��k��0��������Ϊ$\frac{2��}{3}$��
��$\frac{2��}{k}$=$\frac{2��}{3}$��
��k=3��
��y=f��3x��+1=2sin��3x-$\frac{��}{3}$��+1��
��f��3x��=2sin��3x-$\frac{��}{3}$����
��h��x��=2sin��3x-$\frac{��}{3}$��
��x��[0��$\frac{��}{3}$]����3x��[0����]��3x-$\frac{��}{3}$��[-$\frac{��}{3}$��$\frac{2��}{3}$]��
��x=$\frac{��}{3}$ʱ��y=2sin$\frac{2��}{3}$=2��$\frac{\sqrt{3}}{2}$=$\sqrt{3}$��
��Ҫʹ����f��kx��=mǡ��������ͬ�ĸ���
��$\sqrt{3}$��m��2��
���� ������Ҫ�������Ǻ�������ʽ������Լ����Ǻ������ʵĿ��飬�����������A���غͦյ�ֵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��4�� | B�� | ��2��4�� | C�� | ��2��3�� | D�� | ��3��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ӷ� | ���� |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15 | B�� | 21 | C�� | 18 | D�� | 24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2 | B�� | ��2i | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{10}{49}$ | B�� | $\frac{5\sqrt{7}}{14}$ | C�� | $\frac{9}{7}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com