
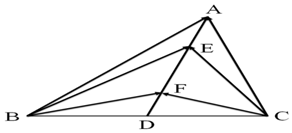
 (2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,
(2)如图,在△ABC中,D是BC的中点,$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,分析 (i)建立坐标系,设C(a,0),A(m,n),求出各向量的坐标,根据条件列出方程组解出a2和m2+n2,从而可得$\overrightarrow{BE}$•$\overrightarrow{CE}$的值;
(ii)设P(λm,λn),根据$\overrightarrow{PA}$•$\overrightarrow{PC}$≥$\overrightarrow{EA}$•$\overrightarrow{EC}$恒成立得出关于λ的不等式恒成立,利用二次函数的性质得出△≤0,从而得出m,n和a的关系,带入距离公式化简即可得出结论.
解答 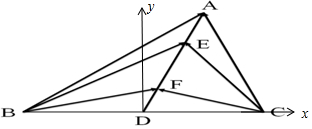 解:(i)∵$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,∴E,F为AD的四等分点.
解:(i)∵$\overrightarrow{AE}$=$\overrightarrow{FD}$=$\frac{1}{4}$$\overrightarrow{AD}$,∴E,F为AD的四等分点.
以BC为x轴,以D为原点建立平面直角坐标系,
设B(-a,0),C(a,0),A(m,n),则E($\frac{3m}{4}$,$\frac{3n}{4}$),F($\frac{m}{4}$,$\frac{n}{4}$),
∴$\overrightarrow{BA}$=(m+a,n),$\overrightarrow{CA}$=(m-a,n),$\overrightarrow{BF}$=($\frac{m}{4}+a$,$\frac{n}{4}$),$\overrightarrow{CF}$=($\frac{m}{4}-a$,$\frac{n}{4}$),$\overrightarrow{BE}$=($\frac{3m}{4}+a$,$\frac{3n}{4}$),$\overrightarrow{CE}$=($\frac{3m}{4}-a$,$\frac{3n}{4}$),
∵$\overrightarrow{BA}$•$\overrightarrow{CA}$=4,$\overrightarrow{BF}$•$\overrightarrow{CF}$=-1,
∴$\left\{\begin{array}{l}{{m}^{2}-{a}^{2}+{n}^{2}=4}\\{\frac{{m}^{2}}{16}-{a}^{2}+\frac{{n}^{2}}{16}=-1}\end{array}\right.$,解得m2+n2=$\frac{16}{3}$,a2=$\frac{4}{3}$.
∴$\overrightarrow{BE}$•$\overrightarrow{CE}$=$\frac{9{m}^{2}}{16}$-a2+$\frac{9{n}^{2}}{16}$=$\frac{9}{16}$(m2+n2)-a2=$\frac{5}{3}$.
(ii)∵P为AD上任一点,设P(λm,λn),则$\overrightarrow{PA}$=((1-λ)m,(1-λ)n),$\overrightarrow{PC}$=(a-λm,-λn),
$\overrightarrow{EA}$=($\frac{m}{4}$,$\frac{n}{4}$),$\overrightarrow{EC}$=(a-$\frac{3m}{4}$,-$\frac{3n}{4}$),
∴$\overrightarrow{PA}•\overrightarrow{PC}$=(1-λ)m(a-λm)-(1-λ)λn2=(1-λ)(ma-λm2-λn2),$\overrightarrow{EA}$•$\overrightarrow{EC}$=$\frac{m}{4}(a-\frac{3m}{4})$-$\frac{3{n}^{2}}{16}$=$\frac{am}{4}$-$\frac{3{m}^{2}}{16}$-$\frac{3{n}^{2}}{16}$.
∵$\overrightarrow{PA}$•$\overrightarrow{PC}$≥$\overrightarrow{EA}$•$\overrightarrow{EC}$恒成立,
∴($\frac{3}{4}$-λ)ma+(λ2-λ+$\frac{3}{16}$)(m2+n2)≥0恒成立,
即(m2+n2)λ2-(m2+n2+ma)λ+$\frac{3}{16}$(m2+n2)+$\frac{3}{4}$ma≥0恒成立,
∴△=(m2+n2+ma)2-4(m2+n2)[$\frac{3}{16}$(m2+n2)+$\frac{3}{4}$ma]≤0,
即$\frac{1}{4}$(m2+n2)2-ma(m2+n2)+m2a2≤0,∴[$\frac{1}{2}$(m2+n2)-ma]2≤0,
∴$\frac{1}{2}$(m2+n2)=ma,即m2-2ma=-n2,
∴AC=$\sqrt{(m-a)^{2}+{n}^{2}}$=$\sqrt{{m}^{2}-2ma+{a}^{2}+{n}^{2}}$=$\sqrt{{a}^{2}}$=a,
又BC=2a,
∴2AC=BC.
点评 本题考查了平面向量的数量积运算,平面向量在几何中的应用,建立坐标系将向量运算转化为坐标运算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $-\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2015) | B. | (-∞,-2019) | C. | (-2015,0) | D. | (-2019,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-$\sqrt{3}$]∪[$\sqrt{3}$,2) | B. | [-2,-$\sqrt{3}$)∪($\sqrt{3}$,2] | C. | [-2,2] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com