
分析 设z=a+bi(其中a,b∈R),则$\overline{z}$=a-bi.利用复数运算和复数相等即可得出答案.
解答 解:设z=a+bi(其中a,b∈R),则$\overline{z}$=a-bi.
由题意得:$\left\{\begin{array}{l}{a+bi-(a-bi)=2i}\\{a-bi=i(a+bi)}\end{array}\right.$,
即$\left\{\begin{array}{l}{bi=i}\\{a-bi=ai-b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$.
∴z=-1+i.
故答案为:-1+i.
点评 本题考查复数代数形式的乘除运算,考查计算能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{14}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
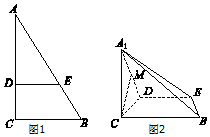 如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=9,D,E分别为AC、AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x,g(x)=($\sqrt{x}$)2 | B. | f(x)=x2,g(x)=(x+1)2 | C. | f(x)=0,g(x)=$\sqrt{x-1}+\sqrt{1-x}$ | D. | f(x)=$\sqrt{{x}^{2}}$,g(x)=|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com