

 (本题满分14分)已知公差不为0的等差数列
(本题满分14分)已知公差不为0的等差数列 的首项
的首项 为
为 (
( ),且
),且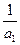 ,
, ,
, 成等比数列(Ⅰ)求数列
成等比数列(Ⅰ)求数列 的通项公式(Ⅱ)对
的通项公式(Ⅱ)对 ,试比较
,试比较 与
与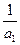 的大小.&
的大小.& 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源:不详 题型:解答题
 和
和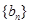 的通项公式分别为
的通项公式分别为 ,
, (
( ),将集合
),将集合 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列 。
。 ;
; 中、但不在数列
中、但不在数列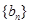 中的项恰为
中的项恰为 ;
; 的通项公式。
的通项公式。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
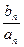 ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
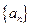 中,
中,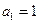 ,
,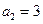 ,其前
,其前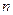 项和为
项和为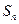 ,且当
,且当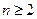 时,
时,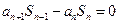 .
.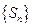 是等比数列;
是等比数列;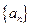 的通项公式;
的通项公式;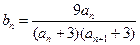 ,记数列
,记数列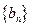 的前
的前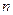 项和为
项和为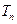 ,证明对于任意的正整数
,证明对于任意的正整数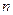 ,都有
,都有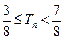 成立.
成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

 的数列
的数列 ,其中
,其中
 .若存在一个正整数
.若存在一个正整数
 ,若数列
,若数列 中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等,则称数列
中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等,则称数列 是“k阶可重复数列”.例如数列
是“k阶可重复数列”.例如数列 :
: 因为
因为 与
与 按次序对应相等,所以数列
按次序对应相等,所以数列 是“4阶可重复数列”.假设数列
是“4阶可重复数列”.假设数列 不是“5阶可重复数列”,若在其最后一项
不是“5阶可重复数列”,若在其最后一项 后再添加一项0或1,均可使新数列是“5阶可重复数列”,且
后再添加一项0或1,均可使新数列是“5阶可重复数列”,且 ,数列
,数列 的最后一项
的最后一项 =______________
=______________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com