
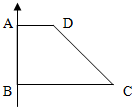
 如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求:
如图1,直角梯形ABCD中,∠A=∠B=90°,AD∥BC,AD=2,AB=3,BC=6,把直角梯形ABCD绕边AB旋转一周得到一个旋转体,求:分析 根据题意知由直角梯形绕其直腰所得的几何体是圆台,根据题意求出圆台的两底面的半径和母线长,再代入表面积和体积公式求解
解答 解:根据题意知由直角梯形绕其直腰所得的几何体是圆台,
其上底面半径r=2,下底面半径R=6,高h=3,故母线l=$\sqrt{{3}^{2}+(6-2)^{2}}$=5,
(1)故该几何体的表面积S=πr2+πR2+πl(r+R)=80π,
(2)该几何体的体积V=$\frac{1}{3}π({r}^{2}+rR+{R}^{2})h$=52π.
点评 本题的考点是旋转体的表面积的求法,关键是由平面图形想象出所得旋转体的结构特征,再求出所得旋转体的高以及其它几何元素的长度,考查了空间想象能力.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 求有关x的方程ax2+bx+c=0的根 | B. | 求函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x,x<0}\end{array}\right.$的值. | ||
| C. | 求1+4+7+10+13的值 | D. | 解不等式ax+b>0(a≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=xlnx | D. | y=x3-2sinx+tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com