
已知函数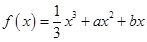
 .
.
(1)若曲线 经过点
经过点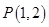 ,曲线
,曲线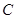 在点
在点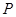 处的切线与直线
处的切线与直线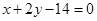 垂直,求
垂直,求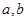 的值;
的值;
(2)在(1)的条件下,试求函数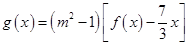 (
(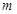 为实常数,
为实常数, )的极大值与极小值之差;
)的极大值与极小值之差;
(3)若 在区间
在区间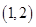 内存在两个不同的极值点,求证:
内存在两个不同的极值点,求证: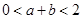 .
.
(1)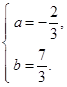
(2)当 或
或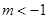 时,
时,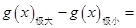
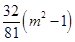 ;
;
当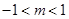 时,
时,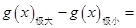
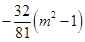 ;
;
(3)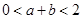 .
.
解析试题分析:(1)利用导数的几何意义,明确曲线
科目:高中数学
来源:
题型:解答题
已知函数f(x)=
科目:高中数学
来源:
题型:解答题
已知函数f(x)=
科目:高中数学
来源:
题型:解答题
已知函数f(x)=ln x+
科目:高中数学
来源:
题型:解答题
已知函数
科目:高中数学
来源:
题型:解答题
经调查统计,某种型号的汽车在匀速行驶中,每小时的耗油量
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区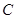 在点
在点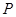 处的切线的斜率为
处的切线的斜率为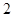 ,建立方程
,建立方程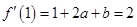 ,再根据曲线
,再根据曲线 经过点
经过点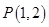 ,得到方程
,得到方程 ,解方程组即得所求.
,解方程组即得所求.
(2)利用“表解法”,确定函数的极值,注意讨论 或
或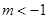 及
及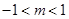 ,的不同情况;
,的不同情况;
(3)根据 在区间
在区间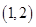 内存在两个极值点,得到
内存在两个极值点,得到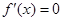 ,
,
即 在
在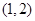 内有两个不等的实根.
内有两个不等的实根.
利用二次函数的图象和性质建立不等式组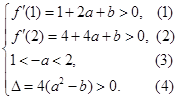 求
求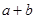 的范围.
的范围.
试题解析:(1)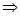
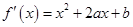 ,
, 直线
直线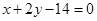 的斜率为
的斜率为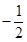 ,
, 曲线
曲线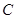 在点
在点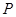 处的切线的斜率为
处的切线的斜率为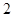 ,
, ①
①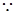 曲线
曲线 经过点
经过点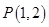 ,
,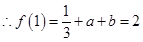 ②
②
由①②得: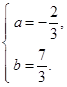 3分
3分
(2)由(1)知: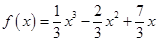 ,
,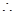
 ,
,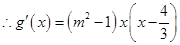 , 由
, 由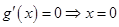 ,或
,或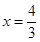 .
.
当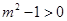 ,即
,即 或
或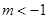 时,
时,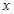 ,
,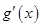 ,
,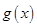 变化如下表
变化如下表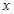
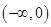

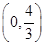
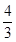
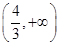
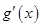
+ 0 

湘教考苑单元测试卷系列答案
精美课堂系列答案
高中同步创新课堂优化方案系列答案
希望全程检测单元测试卷系列答案
全程培优卷系列答案

期末模拟16套系列答案
特优五合卷系列答案

新课堂冲刺100分系列答案
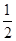 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R.
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间. ax3-
ax3-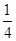 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
(1)求a,c,d的值;
(2)若h(x)=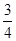 x2-bx+
x2-bx+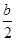 -
-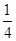 ,解不等式f′(x)+h(x)<0.
,解不等式f′(x)+h(x)<0. -1.
-1.
(1)求函数f(x)的单调区间;
(2)设m∈R,对任意的a∈(-1,1),总存在x0∈[1,e],使得不等式ma-f(x0)<0成立,求实数m的取值范围.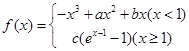 在
在 处存在极值.
处存在极值.
(1)求实数 的值;
的值;
(2)函数 的图像上存在两点A,B使得
的图像上存在两点A,B使得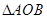 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在 轴上,求实数
轴上,求实数 的取值范围;
的取值范围;
(3)当 时,讨论关于
时,讨论关于 的方程
的方程 的实根个数.
的实根个数.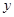 (升)关于行驶速度
(升)关于行驶速度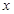 (千米/时)的函数可表示为
(千米/时)的函数可表示为 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为
千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为 (升).
(升).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)讨论函数 的单调性,当
的单调性,当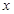 为多少时,耗油量
为多少时,耗油量 为最少?最少为多少升?
为最少?最少为多少升?
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号