
分析 设Ai={一批产品中有i件次品},i=0,1,2,3,4,B={任取10件检查出一件次品},C={产品中次品不超两件},由题意和全概率公式求出P(B)=$\sum_{i=0}^{4}P({A}_{i})P(B|{A}_{i})$=0.196,再由Bayes公式能求出P(C)=$\sum_{i=2}^{2}P({A}_{i}|B)$=0.588.
解答 解:设Ai={一批产品中有i件次品},i=0,1,2,3,4,B={任取10件检查出一件次品},
C={产品中次品不超两件},由题意:
P(B|A0)=$\frac{{C}_{1}^{1}{C}_{49}^{9}}{{C}_{50}^{10}}$=$\frac{1}{5}$,
P(B|A1)=$\frac{{C}_{1}^{1}{C}_{49}^{9}}{{C}_{50}^{10}}$=$\frac{16}{49}$,
P(B|A2)=$\frac{{C}_{2}^{1}{C}_{48}^{9}}{{C}_{50}^{10}}$=$\frac{16}{49}$,
P(B|A3)=$\frac{{C}_{3}^{1}{C}_{48}^{9}}{{{C}_{50}^{10}}_{\;}}$=$\frac{16}{49}$,
P(B|A4)=$\frac{{C}_{4}^{1}{C}_{46}^{9}}{{C}_{50}^{10}}$=$\frac{988}{2303}$,
∵A0,A1,A2,A3,A4构成了完备事件组,
由全概率公式:
P(B)=$\sum_{i=0}^{4}P({A}_{i})P(B|{A}_{i})$=0.196,
由Bayes公式,$P({A}_{0}|B)=\frac{P({A}_{0})P(B|{A}_{0})}{P(B)}$=0,
P(A1|B)=$\frac{P({A}_{1})P(B|{A}_{1})}{P(B)}$=0.255,
P(A2|B)=$\frac{P({A}_{2})P(B|{A}_{2})}{P(B)}$=0.333,
∴P(C)=$\sum_{i=2}^{2}P({A}_{i}|B)$=0.588.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意全概率公式、Bayes公式的合理运用.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
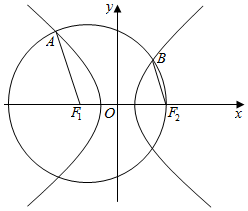 如图,设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,若以F1为圆心,以F1F2为半径的圆与C交于A,B两点(A在第二象限,B在第一象限),且F1A∥F2B,则双曲线C的离心率为( )
如图,设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,若以F1为圆心,以F1F2为半径的圆与C交于A,B两点(A在第二象限,B在第一象限),且F1A∥F2B,则双曲线C的离心率为( )| A. | $\frac{3+\sqrt{17}}{4}$ | B. | 2 | C. | $\frac{1+\sqrt{17}}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{7\sqrt{2}}{10}$ | D. | -$\frac{7\sqrt{2}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com