
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据“和谐函数”的定义,结合函数的单调性,建立条件关系,利用数形结合进行判断即可.
解答 解:由题意知,若f(x)在区间[a,b]上单调递增,须满足:f(a)=$\frac{a}{2}$,f(b)=$\frac{b}{2}$,
若f(x)在区间[a,b]上单调递减,须满足:f(b)=$\frac{a}{2}$,f(a)=$\frac{b}{2}$,
①g(x)=$\sqrt{x-1}$+$\frac{1}{4}$在[1,+∞)为增函数;
则f(a)=$\frac{a}{2}$,f(b)=$\frac{b}{2}$,
即a,b是函数g(x)=$\frac{x}{2}$的两个根,
即$\sqrt{x-1}$+$\frac{1}{4}$=$\frac{x}{2}$,
则$\sqrt{x-1}$=-$\frac{1}{4}$+$\frac{x}{2}$,
作出函数y=$\sqrt{x-1}$和y=-$\frac{1}{4}$+$\frac{x}{2}$的图象如图:
则两个函数有两个交点,满足条件.
②h(x)=${log_{\frac{1}{2}}}$(($\frac{1}{2}$)x+$\frac{1}{8}$)是增函数;
则f(a)=$\frac{a}{2}$,f(b)=$\frac{b}{2}$,
即a,b是函数h(x)=$\frac{x}{2}$的两个根,
即${log_{\frac{1}{2}}}$(($\frac{1}{2}$)x+$\frac{1}{8}$)=$\frac{x}{2}$,
即($\frac{1}{2}$)x+$\frac{1}{8}$=($\frac{1}{2}$)${\;}^{\frac{x}{2}}$=($\frac{\sqrt{2}}{2}$)x,
作出y=($\frac{1}{2}$)x+$\frac{1}{8}$和y=($\frac{\sqrt{2}}{2}$)x,的图象如图: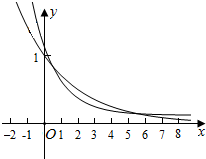
则两个函数有两个交点,满足条件.
③p(x)=$\frac{1}{x}$为减函数;
则p(b)=$\frac{a}{2}$,p(a)=$\frac{b}{2}$,
即$\left\{\begin{array}{l}{\frac{1}{a}=\frac{b}{2}}\\{\frac{1}{b}=\frac{a}{2}}\end{array}\right.$,即ab=2,当a=$\frac{1}{2}$,b=4时,满足条件.
④q(x)=lnx在(0,+∞)为增函数.
则q(a)=$\frac{a}{2}$,q(b)=$\frac{b}{2}$,
即a,b是函数q(x)=$\frac{x}{2}$的两个根,
即lnx=$\frac{x}{2}$,
作出y=lnx和y=$\frac{x}{2}$的图象如图: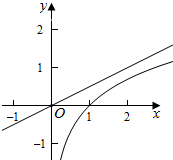
则两个图象没有交点,不满足条件.
故选:C
点评 本题主要考查函数与方程的应用,根据函数定义域和值域的关系,转化为函数与方程的关系,利用数形结合是解决本题的关键.综合性较强.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
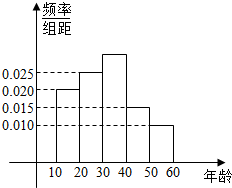 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M⊆N | B. | N⊆M | ||
| C. | M=N | D. | M与N之间没有包含关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com