
分析 (1)设等差数列{an}的公差为d,满足a1=3,a5=15,可得15=3+4d,解得d可得an.由数列{bn}满足b1=4,b5=31,设cn=bn-an,且数列{cn}为等比数列(可设公比为q).可得c1=1,c5=16,利用16=1×q4,可得q,即可得出.
(2)对q分类讨论,利用等比数列与等差数列的前n项和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,满足a1=3,a5=15,
∴15=3+4d,解得d=3.
∴an=3+3(n-1)=3n.
∵数列{bn}满足b1=4,b5=31,设cn=bn-an,且数列{cn}为等比数列(可设公比为q).
∴c1=4-3=1,c5=31-15=16,
∴16=1×q4,
解得q=±2,
∴${c}_{n}=(±2)^{n-1}$.
∴bn=an+cn=3n+(±2)n-1.
(2)当q=2时,数列{bn}的前n项和=$\frac{n(3+3n)}{2}$+$\frac{{2}^{n}-1}{2-1}$=$\frac{3({n}^{2}+n)}{2}$+2n-1.
当q=-2时,数列{bn}的前n项和=$\frac{n(3+3n)}{2}$+$\frac{(-2)^{n}-1}{-2-1}$=$\frac{3({n}^{2}+n)}{2}$-$\frac{1}{3}[(-2)^{n}-1]$.
点评 本题考查了等差数列等比数列的通项公式及其前n项和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
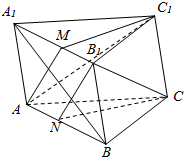 如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1,③平面AMC1∥平面CNB1,其中正确结论的个数为( )
如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1,③平面AMC1∥平面CNB1,其中正确结论的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | (0,4] | C. | $(0,\frac{1}{4}]$ | D. | $[\frac{1}{4},4]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com