Question

20．如图所示，要测量河两岸P，Q两点之间的距离，在与点P同侧的岸边选取了A，B两点（A，B，P，Q四点在同一平面内）．并测得AP=20m，BP=10m，∠APB=60°，∠PAQ=105°，∠PBQ=135°．试求P，Q两点之间的距离．

Answer 1

分析 连结AB，在△APB中分别由余弦、正弦定理求出未知的边和角，由条件求出∠BAQ、∠ABQ，在△ABQ中分别由正弦、余弦定理求出AQ和PQ即可．

解答 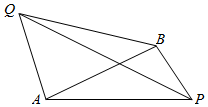解：连结AB，如图：
在△APB中，由余弦定理得，
AB²=AP²+BP²-2AP×BP×cos∠APB
=400+100-2×20×10×$\frac{1}{2}$=300，
则AB=10$\sqrt{3}$（m），
由正弦定理得，$\frac{AB}{sin∠APB}=\frac{AP}{sin∠ABP}$，
则$\frac{10\sqrt{3}}{\frac{\sqrt{3}}{2}}=\frac{20}{sin∠ABP}$，得sin∠ABP=1，即∠ABP=90°，所以∠BAP=180°-90°-30°=60°，
因为∠PAQ=105°，∠PBQ=135°，所以∠BAQ=75°，∠ABQ=45°，
则∠BQA=180°-75°-45°=60°，
在△ABQ中，由正弦定理得$\frac{AQ}{sin∠ABQ}=\frac{AB}{sin∠AQB}$，
则$\frac{AQ}{\frac{\sqrt{2}}{2}}=\frac{10\sqrt{3}}{\frac{\sqrt{3}}{2}}$，解得AQ=10$\sqrt{2}$（m），
在△APQ中，PQ²=AP²+AQ²-2AP×AQ×cos∠QAP
=400+200-2×20×10$\sqrt{2}$×（-$\frac{\sqrt{6}-\sqrt{2}}{4}$）
=400+200$\sqrt{3}$=100（4+2$\sqrt{3}$）=100$（1+\sqrt{3}）^{2}$，
所以PQ=10（$\sqrt{3}$+1）（m），
故P，Q两点之间的距离是10（$\sqrt{3}+1$）m．

点评 本题考查了余弦、正弦定理在实际中的综合应用，考查化简、计算能力，属于中档题．