
(本小题满分13分)已知数列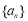 的前n项和为
的前n项和为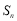 ,
,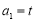 (
(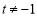 ),
),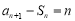 .
.
(1)当t为何值时,数列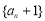 是等比数列?
是等比数列?
(2)设数列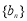 的前n项和为
的前n项和为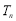 ,
, 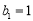 ,点
,点 在直线
在直线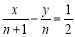 上,在(1)的条件下,若不等式
上,在(1)的条件下,若不等式 对于
对于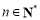 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
(1)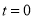 时,数列
时,数列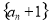 是等比数列;(2)
是等比数列;(2)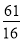 .
.
【解析】
试题分析:(1)给出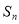 与
与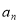 的关系,求
的关系,求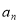 ,常用思路:一是利用
,常用思路:一是利用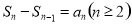 转化为
转化为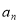 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为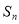 的递推关系,先求出
的递推关系,先求出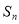 与
与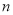 的关系,再求
的关系,再求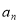 ;由
;由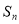 推
推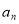 时,别漏掉
时,别漏掉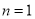 这种情况,大部分学生好遗忘;(2)一般地,如果数列
这种情况,大部分学生好遗忘;(2)一般地,如果数列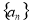 是等差数列,
是等差数列, 是等比数列,求数列
是等比数列,求数列
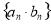 的前
的前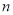 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列 的公比,然后做差求解;(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
的公比,然后做差求解;(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
试题解析:(1)由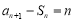 ,得
,得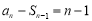 (
(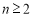 ),
),
两式相减得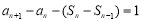 ,即
,即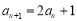 , 1分
, 1分
所以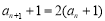 (
(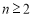 ), 2分
), 2分
由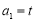 及
及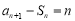 ,得
,得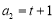 ,
,
:]因为数列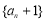 是等比数列,所以只需要
是等比数列,所以只需要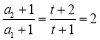 ,解得
,解得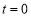 ,此时,数列
,此时,数列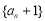 是以
是以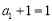 为首项,2为公比的等比数列. 4分
为首项,2为公比的等比数列. 4分
(2)由(1)得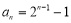 ,因为点
,因为点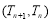 在直线
在直线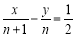 上,所以
上,所以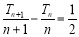 ,
,
故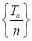 是以
是以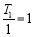 为首项,
为首项,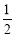 为公差的等差数列,则
为公差的等差数列,则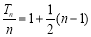 ,所以
,所以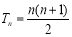 ,
,
当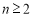 时,
时,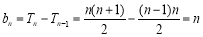 ,
,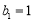 满足该式,所以
满足该式,所以 . 6分
. 6分
不等式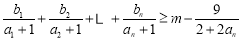 ,即为
,即为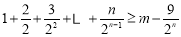 ,
,
令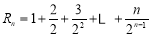 ,则
,则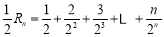 ,两式相减得
,两式相减得
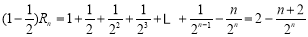 ,所以
,所以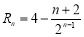 . 10分
. 10分
由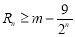 恒成立,即
恒成立,即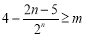 恒成立,又
恒成立,又 ,
,
故当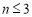 时,
时,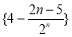 单调递减;当
单调递减;当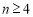 时,
时,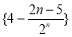 单调递增,
单调递增,
当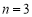 时,
时,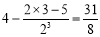 ;当
;当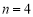 时,
时,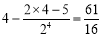 ,则
,则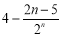 的最小值为
的最小值为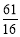 ,所以实数
,所以实数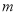 的最大值是
的最大值是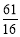 . 13分
. 13分
考点:1、证明数列是等比数列;2、错位相减求数列的和;3、恒成立的问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试理科数学试卷(解析版) 题型:填空题
已知定义在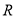 上的函数
上的函数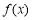 的图象连续不断,若存在常数
的图象连续不断,若存在常数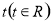 ,使得
,使得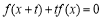 对任意的实数x成立,则称f(x)是回旋函数,其回旋值为t.给出下列四个命题:
对任意的实数x成立,则称f(x)是回旋函数,其回旋值为t.给出下列四个命题:
①函数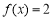 为回旋函数的充要条件是回旋值t=-1;
为回旋函数的充要条件是回旋值t=-1;
②若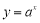 (a>0,且a≠1)为回旋函数,则回旋值t>1;
(a>0,且a≠1)为回旋函数,则回旋值t>1;
③若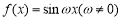 为回旋函数,则其最小正周期不大于2;
为回旋函数,则其最小正周期不大于2;
④对任意一个回旋值为t(t≥0)的回旋函数f(x),方程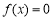 均有实数根.
均有实数根.
其中为真命题的是_____________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试理科数学试卷(解析版) 题型:选择题
若执行下面的程序框图,输出 的值为3,则判断框中应填入的条件是
的值为3,则判断框中应填入的条件是

(A) (B)
(B)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2015届四川省资阳市高三第一次诊断性测试文科数学试卷(解析版) 题型:填空题
已知函数f(x)是定义域为R的奇函数,且周期为2,若当x∈[0,1)时,f(x)=2x-1,则f(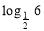 )的值是________________.
)的值是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com