
对于任意![]() ,比较
,比较![]() 与
与![]() 的大小,并用数学归纳法证明你的结论.
的大小,并用数学归纳法证明你的结论.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
| bn |
| an |
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| T3 |
| 1 |
| Tn |
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高一下学期期中考试数学 题型:解答题
设等比数列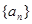 的前n项和为
的前n项和为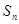 ,等差数列
,等差数列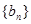 的前n项和为
的前n项和为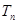 ,已知
,已知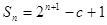 (其中
(其中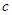 为常数),
为常数),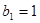 ,
,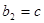 。
。
(1)求常数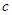 的值及数列
的值及数列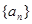 ,
,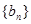 的通项公式
的通项公式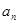 和
和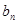 。
。
(2)设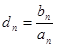 ,设数列
,设数列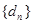 的前n项和为
的前n项和为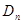 ,若不等式
,若不等式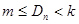 对于任意的
对于任意的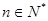 恒成立,求实数m的最大值与整数k的最小值。
恒成立,求实数m的最大值与整数k的最小值。
(3)试比较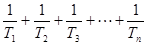 与2的大小关系,并给出证明。
与2的大小关系,并给出证明。
查看答案和解析>>
科目:高中数学 来源:0107 期中题 题型:解答题
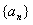 的前n项和为
的前n项和为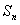 ,等差数列
,等差数列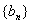 的前n项和为
的前n项和为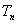 ,已知
,已知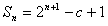 (其中c为常数),
(其中c为常数),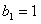 ,
,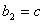 。
。  ,
,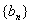 的通项公式
的通项公式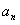 和
和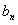 。
。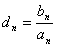 ,设数列
,设数列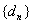 的前n项和为
的前n项和为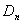 ,若不等式
,若不等式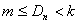 对于任意
对于任意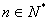 的恒成立,求实数m的最大值与整数k的最小值。
的恒成立,求实数m的最大值与整数k的最小值。 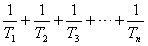 与2的大小关系,并给出证明。
与2的大小关系,并给出证明。 查看答案和解析>>
科目:高中数学 来源:2009-2010学年吉林省实验中学高一(下)期中数学试卷(必修5)(解析版) 题型:解答题
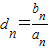 ,设数列dn的前n项和为Dn,若不等式m≤Dn<k对于任意的n∈N*恒成立,求实数m的最大值与整数k的最小值.
,设数列dn的前n项和为Dn,若不等式m≤Dn<k对于任意的n∈N*恒成立,求实数m的最大值与整数k的最小值.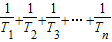 与2的大小关系,并给出证明.
与2的大小关系,并给出证明.查看答案和解析>>
科目:高中数学 来源:广东省汕头市08-09学年高二新课程期末统一检测(理) 题型:解答题
从曲线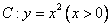 上一点
上一点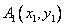 引曲线C的第一条切线
引曲线C的第一条切线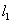 ,
,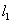 交
交 轴于点
轴于点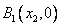 ,过点
,过点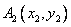 引曲线C的第二条切线
引曲线C的第二条切线 ,
, 交
交 轴于点
轴于点 ,…如此反复作下去,由切线
,…如此反复作下去,由切线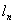 得到点列
得到点列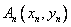 ,
,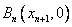 ,
,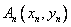 的横坐标组成数列
的横坐标组成数列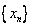 ,
,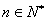
(1)若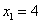 ,求数列
,求数列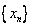 的通项公式;
的通项公式;
(2)若对于任意的正整数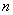 都有
都有 恒成立,且
恒成立,且 ,求
,求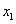 的最大值;
的最大值;
(3)在(1)的条件下,记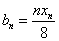 ,数列
,数列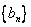 的前
的前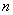 项和为
项和为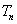 ,试比较
,试比较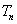 与1的大小。
与1的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com