
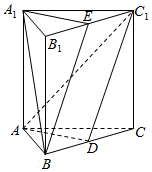
 如图,正三棱柱ABC-A1B1C1中,点D为BC的中点.
如图,正三棱柱ABC-A1B1C1中,点D为BC的中点.分析 (1)由AD⊥BC,AD⊥CC1即可得出AD⊥平面BCC1B1;
(2)由四边形BDC1E位平行四边形可得出BE∥C1D,故而BE∥平面ADC1.
解答 证明:(1)∵CC1⊥平面ABC,AD?平面ABC,
∴AD⊥CC1,
∵△ABC是等边三角形,D是BC的中点,
∴AD⊥BC,
又BC?平面BCC1B1,CC1?平面BCC1B1,BC∩CC1=C,
∴AD⊥平面BCC1B1.
(2)∵D,E分别是BC,B1C1的中点,BC$\stackrel{∥}{=}$B1C1,
∴BD$\stackrel{∥}{=}$C1E,
∴四边形BDC1E是平行四边形,
∴BE∥C1D,
又BE?平面AC1D,C1D?平面AC1D,
∴BE∥平面AC1D.
点评 本题考查了线面平行,线面垂直的判定,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | ${y^2}=\frac{{16\sqrt{3}}}{3}x$ | B. | ${y^2}=\frac{{8\sqrt{3}}}{3}x$ | C. | y2=16x | D. | y2=8x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不及格 | 及格 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
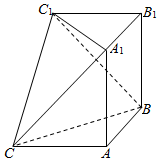 如图,AA1,BB1均垂直于平面ABC和平面A1B1C1,∠BAC=∠A1B1C1=90°,AC=AB=A1A=B1C1=$\sqrt{2}$,则多面体ABC-A1B1C1的外接球的表面积为( )
如图,AA1,BB1均垂直于平面ABC和平面A1B1C1,∠BAC=∠A1B1C1=90°,AC=AB=A1A=B1C1=$\sqrt{2}$,则多面体ABC-A1B1C1的外接球的表面积为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 以上都可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
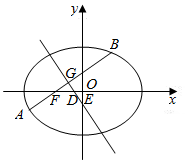 椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左焦点为F,右顶点为A1,过点F斜率为k的直线交椭圆C于A,B两点,线段AB的中点为G,线段AB的垂直平分线交x轴于点D,交y轴于点E,O是坐标原点,记△GFD的面积为S1,记△OED的面积为S2
椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1的左焦点为F,右顶点为A1,过点F斜率为k的直线交椭圆C于A,B两点,线段AB的中点为G,线段AB的垂直平分线交x轴于点D,交y轴于点E,O是坐标原点,记△GFD的面积为S1,记△OED的面积为S2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com