
【题目】已知函数 ![]() .
.
(I)若 ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() ,求
,求 ![]() 的值;
的值;
(II)若 ![]() 在
在 ![]() 上为增函数,求
上为增函数,求 ![]() 得取值范围.
得取值范围.
【答案】解:(I)因为 ![]() ,又
,又 ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() ,
,
所以 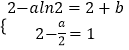 所以
所以 ![]()
(II)因为 ![]() 在
在 ![]() 上为增函数,
上为增函数,
所以 ![]() 在
在 ![]() 上恒成立.
上恒成立.
即 ![]() 在
在 ![]() 上恒成立,所以有
上恒成立,所以有 ![]() .
.
【解析】(1)根据切线的斜率为1,得到f'(2)=1,解之得a=2;从而得到f(x)=![]() x2-2lnx,算出切点坐标为(2,2-2ln2),再代入直线y=x+b,即可求出实数b的值.
x2-2lnx,算出切点坐标为(2,2-2ln2),再代入直线y=x+b,即可求出实数b的值.
(2)根据题意,f'(x)≥0在(1,+∞)上恒成立,由此得到关于x的不等式a≤x2在(1,+∞)上恒成立,再讨论x2的取值范围,即可得到a的取值范围.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗.2018年春节前夕, ![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标,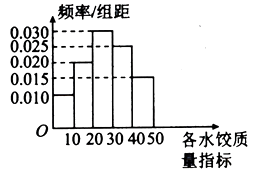
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值 ![]() 服从正态分布
服从正态分布 ![]() ,利用该正态分布,求
,利用该正态分布,求 ![]() 落在
落在 ![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于 ![]() 内的包数为
内的包数为 ![]() ,求
,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为 ![]() ;
;
②若 ![]() ,则
,则 ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R,且e为自然对数的底数).
(1)判断函数f(x)的单调性与奇偶性;
(2)是否存在实数t , 使不等式f(x-t)+f(x2-t2)≥0对一切x∈R都成立?若存在,求出t;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上动点 ![]() 与两个定点
与两个定点 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求点 ![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中轨迹为 ![]() ,过点
,过点 ![]() 的直线
的直线 ![]() 被
被 ![]() 所截得的线段长度为8,求直线
所截得的线段长度为8,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰直角△ABO中,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,|
,| ![]() |=|
|=| ![]() |=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,
|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点, ![]() =
= ![]() ,则
,则 ![]() (
( ![]() ﹣
﹣ ![]() )=( )
)=( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,设
,设 ![]() .
.
(Ⅰ)若f(α)=2,求 ![]() 的值;
的值;
(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣b)cosC=ccosB,求f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人到甲、乙两市各 ![]() 个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )
个小区调查空置房情况,调查得到的小区空置房的套数绘成了如图的茎叶图,则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为( )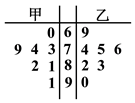
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
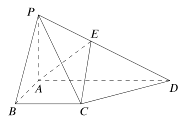
【题目】如图,在四棱锥 ![]() 中,底面
中,底面 ![]() 为直角梯形,
为直角梯形, ![]() ,且
,且 ![]() ,
, ![]() 平面
平面 ![]() .
.
(1)求 ![]() 与平面
与平面 ![]() 所成角的正弦值;
所成角的正弦值;
(2)棱 ![]() 上是否存在一点
上是否存在一点 ![]() 满足
满足 ![]() ?若存在,求
?若存在,求 ![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com